题目内容
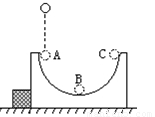
 如图所示,置于光滑水平面上的A、B、C是三个质量均为m=2.0kg的相同物块.A、B与一轻弹簧固定连接,用一轻绳把A、B拉近后梆紧,使弹簧处于缩短状态,两物块保持静止.物块C以大小为v0=6.0m/s的初速向右运动,当C与B发生碰撞时二者立刻靠在一起运动但不粘连.C与B发生碰撞后弹簧长度又再缩短、然后才逐渐恢复,并在这个过程将轻绳剪断,当弹簧伸长至自身的自然长度时,C的速度恰好为零.设C与B碰撞时的撞击力比弹簧的弹力大得多,弹簧的形变都在弹性范围内,求:
如图所示,置于光滑水平面上的A、B、C是三个质量均为m=2.0kg的相同物块.A、B与一轻弹簧固定连接,用一轻绳把A、B拉近后梆紧,使弹簧处于缩短状态,两物块保持静止.物块C以大小为v0=6.0m/s的初速向右运动,当C与B发生碰撞时二者立刻靠在一起运动但不粘连.C与B发生碰撞后弹簧长度又再缩短、然后才逐渐恢复,并在这个过程将轻绳剪断,当弹簧伸长至自身的自然长度时,C的速度恰好为零.设C与B碰撞时的撞击力比弹簧的弹力大得多,弹簧的形变都在弹性范围内,求:(1)弹簧初始状态时的弹性势能.
(2)在碰撞后的运动过程中,物块B的速度最大值.
分析:(1)C与B碰撞过程,两物体的动量守恒.由动量守恒定律求出碰后共同速度.轻绳断开到弹簧伸长至自身的自然长度的过程中,C的速度恰好为零,B的速度也为零,根据系统的动量守恒求此时A的速度,由系统的机械能守恒定律求解弹簧初始状态时的弹性势能.
(2)弹簧恢复到原长后以后,C与B分离,B在弹簧作用下向右加速运动,当弹簧长度第二次恢复自然长度时,物块B的速度达到最大值.根据A、B、弹簧组成的系统动量守恒和机械
能守恒,列式,可求出B的速度最大值.
(2)弹簧恢复到原长后以后,C与B分离,B在弹簧作用下向右加速运动,当弹簧长度第二次恢复自然长度时,物块B的速度达到最大值.根据A、B、弹簧组成的系统动量守恒和机械
能守恒,列式,可求出B的速度最大值.
解答:解:(1)C与B碰撞过程,由动量守恒定律得
mv0=2mv1 ①
代入数据解得C、B碰后的共同速度
v1=3.0m/s ②
轻绳断开到弹簧伸长至自身的自然长度这一过程,由动量守恒定律得
2mv1=0+mvA ③
代入数据解得此时A的速度
vA=6.0m/s ④
由机械能守恒定律得
?2mv12+Ep=0+
m
⑤
代入数据解得弹簧初始状态时的弹性势能
Ep=18J ⑥
(2)以后,C与B分离,B在弹簧作用下向右加速运动,当弹簧长度第二次恢复自然长度时,物块B的速度达到最大值.
设弹簧长度第二次恢复自然长度时,A和B的速度各为v′A、v′B,在这一过程中,对A和B组成的系统,由动量守恒定律得
mvA=mv′A+mv′B ⑦
由机械能守恒定律得
m
=
mv
+
mv
⑧
代入数据解得
v′A=0,v′B=6.0m/s ⑨
因此B的最大速度为6.0m/s
答:
(1)弹簧初始状态时的弹性势能为18J.
(2)在碰撞后的运动过程中,物块B的速度最大值为6.0m/s.
mv0=2mv1 ①
代入数据解得C、B碰后的共同速度
v1=3.0m/s ②
轻绳断开到弹簧伸长至自身的自然长度这一过程,由动量守恒定律得
2mv1=0+mvA ③
代入数据解得此时A的速度
vA=6.0m/s ④
由机械能守恒定律得
| 1 |
| 2 |
| 1 |
| 2 |
| v | 2 A |
代入数据解得弹簧初始状态时的弹性势能
Ep=18J ⑥
(2)以后,C与B分离,B在弹簧作用下向右加速运动,当弹簧长度第二次恢复自然长度时,物块B的速度达到最大值.
设弹簧长度第二次恢复自然长度时,A和B的速度各为v′A、v′B,在这一过程中,对A和B组成的系统,由动量守恒定律得
mvA=mv′A+mv′B ⑦
由机械能守恒定律得
| 1 |
| 2 |
| v | 2 A |
| 1 |
| 2 |
| ′ | 2 A |
| 1 |
| 2 |
| ′ | 2 B |
代入数据解得
v′A=0,v′B=6.0m/s ⑨
因此B的最大速度为6.0m/s
答:
(1)弹簧初始状态时的弹性势能为18J.
(2)在碰撞后的运动过程中,物块B的速度最大值为6.0m/s.
点评:本题关键要分析物体运动的过程,抓住碰撞过程系统的动量守恒,碰撞后系统的机械能守恒列式,即可进行求解.

练习册系列答案
 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案
相关题目

 (1)在“探究求合力的方法”时,先将橡皮条的一端固定在水平木板上,另一端系上带有绳套的两根细绳.实验时,先后两次拉伸橡皮条,一次是用两个弹簧秤通过两细绳互成角度地拉橡皮条,另一次是用一个弹簧秤通过细绳拉橡皮条.在本实验中,下列说法正确的是
(1)在“探究求合力的方法”时,先将橡皮条的一端固定在水平木板上,另一端系上带有绳套的两根细绳.实验时,先后两次拉伸橡皮条,一次是用两个弹簧秤通过两细绳互成角度地拉橡皮条,另一次是用一个弹簧秤通过细绳拉橡皮条.在本实验中,下列说法正确的是 出间距d.开始时将木板置于MN处,现缓慢向瓶中加水,直到木板刚刚开始运动为止,记下弹簧秤的示数F0,以此表示滑动摩擦力的大小.再将木板放回原处并按住,继续向瓶中加水后,记下弹簧秤的示数F1,然后释放木板,并用秒表记下木板运动到PQ处的时间t. ①木板的加速度可以用d、t表示为a=
出间距d.开始时将木板置于MN处,现缓慢向瓶中加水,直到木板刚刚开始运动为止,记下弹簧秤的示数F0,以此表示滑动摩擦力的大小.再将木板放回原处并按住,继续向瓶中加水后,记下弹簧秤的示数F1,然后释放木板,并用秒表记下木板运动到PQ处的时间t. ①木板的加速度可以用d、t表示为a=