题目内容
（2009?孝感模拟）如图所示的靠轮传动装置中右轮半径为2r，a为它边缘上的一点，b为轮上的一点，b距轴为r．左侧为一轮轴，大轮的半径为4r，d为它边缘上的一点，小轮的半径为r，c为它边缘上的一点．若传动中靠轮不打滑，则（ ）
分析：c、d轮共轴转动，角速度相等，b、c两轮在传动中靠轮不打滑，知b、c两轮边缘上的点线速度大小相等．根据线速度与角速度、向心加速度的关系比较它们的大小．
解答：解：A、c、d轮共轴转动，角速度相等，根据v=rω知，d点的线速度大于c点的线速度，而a、c的线速度大小相等，a、b的角速度相等，则a的线速度大于b的线速度，所以d点的线速度大于b点的线速度．故A错误，B正确．
C、a、c的线速度相等，半径比为2：1，根据ω=
，知a、c的角速度之比1：2．a、b的角速度相等，所以b、c的角速度不等．故C错误．
D、a、c的线速度相等，半径比为2：1，根据a=
，知向心加速度之比为1：2．c、d的角速度相等，根据a=rω2，知c、d的向心加速度之比为1：4，所以a、d两点的向心加速度之比为1：8．故D正确．
故选BD．
C、a、c的线速度相等，半径比为2：1，根据ω=
| v |
| r |
D、a、c的线速度相等，半径比为2：1，根据a=
| v2 |
| r |
故选BD．
点评：解决本题的关键知道共轴转动，角速度相等，不打滑传动，轮子边缘上的点线速度大小相等．
练习册系列答案
名校联盟快乐课堂系列答案
黄冈创优卷系列答案
相关题目
（2009?孝感模拟）一光滑圆环固定在竖直平面内，环上套着两个小球A和B（中央有孔），A、B间由细绳连接着，它们处于如图中所示位置时恰好都能保持静止状态．此情况下，B球与环中心O处于同一水平面上，AB间的细绳呈伸直状态，与水平线成300夹角．已知B球的质量为m，求：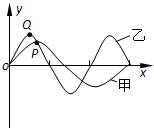
（2009?孝感模拟）如图所示为某时刻从O点同时持续发出的两列简谐横波在同一介质中沿相同方向传播的波形图，P点在甲波最大位移处，Q点在乙波的最大位移处，下列说法正确的是（ ）
（2009?孝感模拟）如图所示，空间存在相互垂直的匀强电场和匀强磁场，电场的方向竖直向下，磁场方向水平（图中垂直纸面向里），一带电油滴P恰好处于静止状态，则下列说法正确的是（ ）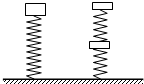
（2009?孝感模拟）如图所示，一根轻质弹簧竖直放在桌面上，下端固定，上端放一重物m，稳定后弹簧长为L；现将弹簧截成等长的两段，将重物分成两块，如图所示连接后，稳定时两段弹簧的总长为L′，则（ ）