题目内容
14.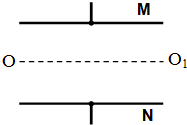 如图所示,水平放置的平行板电容器极板间距离为d,上极板带正电.现有一束微粒以某一速度垂直于电场方向沿中心线OO1射入,当加的电压为U0时,微粒能沿OO1水平飞出电场.当电压升高到U1时,微粒可以从距M板$\frac{d}{4}$处飞出电场.求:
如图所示,水平放置的平行板电容器极板间距离为d,上极板带正电.现有一束微粒以某一速度垂直于电场方向沿中心线OO1射入,当加的电压为U0时,微粒能沿OO1水平飞出电场.当电压升高到U1时,微粒可以从距M板$\frac{d}{4}$处飞出电场.求:(1)带电微粒的比荷是多少?带何种电荷?
(2)要使微粒束能从距N板$\frac{d}{4}$处飞出电场,则所加的电压U2应为多少?
分析 (1)由题,平行板电容器极板间电压为U0时,微粒沿水平方向飞出电场,说明微粒受力平衡,根据平衡条件求解带电微粒的比荷,并确定微粒的电性.
(2)题中,当电压升高到U1时,微粒可以从距M板$\frac{d}{4}$处飞出电场,要使微粒束能从距N板$\frac{d}{4}$处飞出电场,两次类平抛运动偏转的位移大小相等,根据牛顿第二定律研究电压U2与U1的关系,并求出U2.
解答 解:
(1)当电压为U0时,微粒受力平衡,则有
mg=$\frac{q{U}_{0}}{d}$
解得$\frac{q}{m}=\frac{gd}{{U}_{0}}$
由于电容器上极板带正电,电场方向向下,微粒所受电场力方向向上,因此微粒带负电.
(2)据题,由于微粒两次偏转的位移大小相同,运动时间相等,因此可知两次运动的加速度大小相同,根据牛顿第二定律得到,竖直方向的合外力大小相同.
即$\frac{q{U}_{1}}{d}$-mg=mg-$\frac{q{U}_{2}}{d}$
得到${U}_{2}=\frac{2mgd}{q}-{U}_{1}$=2U0-U1
答:
(1)带电微粒的比荷$\frac{q}{m}=\frac{gd}{{U}_{0}}$,带负电荷.
(2)要使微粒束能从距N板$\frac{d}{4}$处飞出电场,所加的电压U2应为2U0-U1.
点评 本题第(2)问是带电粒子在电场中类平抛运动的问题,抓住两次轨迹的对称性是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
4.动能的单位是什么?( )
| A. | 米 | B. | 米每秒 | C. | 千瓦 | D. | 焦耳 |
5.有一种高速磁悬浮列车的设计方案是在每节车厢底部安装强磁铁(磁场方向向下),并在两条铁轨之间沿途平放一系列线圈.通过车厢底部强磁铁的运动,使线圈中磁通量发生变化,从而在线圈中产生感应电流,而感应电流的磁场与强磁铁磁场发生作用,使列车浮起.对于其中原理,下列说法中错误的是( )
| A. | 当列车运动时,通过线圈的磁通量会发生变化 | |
| B. | 列车速度越快,通过线圈的磁通量变化越快 | |
| C. | 列车运动时,线圈中会产生感应电流 | |
| D. | 线圈中感应电流的大小与列车速度无关 |
2.下述说法中正确的是( )
| A. | 电场线是实际存在的,与电荷运动的轨迹是一致的 | |
| B. | 由U=Ed可知,匀强电场中的任意两点a、b间的距离越大,则两点间的电势差也一定越大 | |
| C. | 元电荷就是电子 | |
| D. | 无论正电荷还是负电荷,克服电场力做功电势能都增大 |
9.下列说法正确的是( )
| A. | 元电荷是表示跟电子所带电荷量数值相等的电荷量 | |
| B. | 带电体体积很大时不能看成点电荷 | |
| C. | 摩擦起电说明电荷可以被创造 | |
| D. | 根据场强叠加原理,可知合电场的场强一定大于分电场的场强 |
19.匀变速直线运动中,加速度a、初速度V0、末速度Vt、时间t、位移x之间关系正确的是( )
| A. | x=$\frac{1}{2}$at2 | B. | x=V0t | C. | x=v0t+$\frac{1}{2}$at2 | D. | x=(V0+Vt)$\frac{t}{2}$ |
6.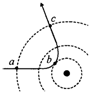 历史上英国物理学家卢瑟福根据α粒子(氦原子核)散射实验,提出了原子的核式结构模型.图中虚线表示原子核所形成的电场的等势线,实线表示一个α粒子的运动迹.在α粒子从a运动到b再运动到c的过程中,下列说法中正确的是( )
历史上英国物理学家卢瑟福根据α粒子(氦原子核)散射实验,提出了原子的核式结构模型.图中虚线表示原子核所形成的电场的等势线,实线表示一个α粒子的运动迹.在α粒子从a运动到b再运动到c的过程中,下列说法中正确的是( )
 历史上英国物理学家卢瑟福根据α粒子(氦原子核)散射实验,提出了原子的核式结构模型.图中虚线表示原子核所形成的电场的等势线,实线表示一个α粒子的运动迹.在α粒子从a运动到b再运动到c的过程中,下列说法中正确的是( )
历史上英国物理学家卢瑟福根据α粒子(氦原子核)散射实验,提出了原子的核式结构模型.图中虚线表示原子核所形成的电场的等势线,实线表示一个α粒子的运动迹.在α粒子从a运动到b再运动到c的过程中,下列说法中正确的是( )| A. | 动能先增大,后减小 | |
| B. | 电势能先减小,后增大 | |
| C. | 电场力先做负功,后做正功,总功等于零 | |
| D. | 加速度先变大,后变小 |
3.上爬和下滑时,他受到摩擦力分别为f1和f2,则( )
| A. | f1方向向下,f2方向向上,且f1=f2 | B. | f1方向向下,f2方向向上,且f1>f2 | ||
| C. | f1方向向上,f2方向向上,且f1=f2 | D. | f1方向向下,f2方向向下,且f1=f2 |