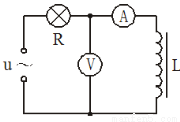
题目内容
14.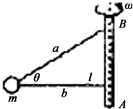 质量为m的小球由轻绳a和b分别系于一轻质细杆的A点和B点,如图所示,绳a与水平方向成θ角,绳b沿水平方向且长为l,当轻杆绕轴AB以角速度ω匀速转动时,小球在水平面内做匀速圆周运动,则下列说法正确的是( )
质量为m的小球由轻绳a和b分别系于一轻质细杆的A点和B点,如图所示,绳a与水平方向成θ角,绳b沿水平方向且长为l,当轻杆绕轴AB以角速度ω匀速转动时,小球在水平面内做匀速圆周运动,则下列说法正确的是( )| A. | a绳张力不可能为零 | |
| B. | a绳的张力随角速度的增大而增大 | |
| C. | 当角速度ω>$\sqrt{\frac{gcosθ}{l}}$,b绳将出现弹力 | |
| D. | 若b绳突然被剪断,a绳的弹力可能不变 |
分析 小球做匀速圆周运动,在竖直方向上的合力为零,水平方向合力提供向心力,结合牛顿第二定律分析判断
解答 解:A、小球做匀速圆周运动,在竖直方向上的合力为零,水平方向上的合力提供向心力,所以a绳在竖直方向上的分力与重力相等,可知a绳的张力不可能为零,故A正确.
B、根据竖直方向上平衡得,Fasinθ=mg,解得Fa=$\frac{mg}{sinθ}$,可知a绳的拉力不变,故B错误.
C、当b绳拉力为零时,有:mgcotθ=mlω2,解得ω=$\sqrt{\frac{gcotθ}{l}}$,可知当角速度ω>$\sqrt{\frac{gcotθ}{l}}$时,b绳出现弹力.故C正确.
D、由于b绳可能没有弹力,故b绳突然被剪断,a绳的弹力可能不变,故D正确.
故选:ACD.
点评 解决本题的关键知道小球做圆周运动向心力的来源分析,知道小球竖直方向合力为零,这是解决本题的关键

练习册系列答案
 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
7.某同学在研究小车的运动实验中,获得一条点迹清楚的纸带,如图所示,已知打点计时器每隔0.02s打一个点,A,B,C,D,E,F各计数点之间有4个点未画出,对计数点进行测量的结果记录在图中,单位是cm.
①计算表空格中的速度大小
②以A为计时起点,在坐标纸上画出小车的v-t图象
③将图线延长与纵轴相交,交点的速度是0.20m/s,此速度的物理意义是零时刻小车经过A点的速度.
④根据图象可求得a=2.0m/s2
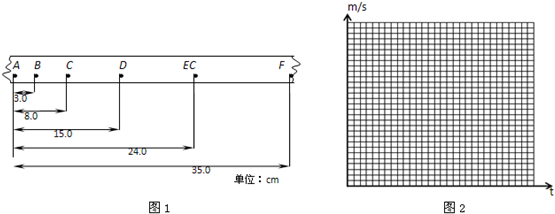
①计算表空格中的速度大小
| 位置 | B | C | D | E |
| 速度m/s | 0.40 | 0.60 |
③将图线延长与纵轴相交,交点的速度是0.20m/s,此速度的物理意义是零时刻小车经过A点的速度.
④根据图象可求得a=2.0m/s2

2.下列说法不符合物理学史实的是( )
| A. | 库仑通过扭秤实验发现了库仑定律 | |
| B. | 在研究电磁现象时,安培引入了“场”的概念 | |
| C. | 奥斯特最早发现电流周围存在磁场 | |
| D. | 伽利略通过理想实验,说明物体的运动不需要力来维持 |
19. 平行厚玻璃板放在空气中,一束复色光从玻璃板下表面斜向上射出,变成a、b两束单色光,如图所示.对于a、b两束光,下面说法正确的是( )
平行厚玻璃板放在空气中,一束复色光从玻璃板下表面斜向上射出,变成a、b两束单色光,如图所示.对于a、b两束光,下面说法正确的是( )
 平行厚玻璃板放在空气中,一束复色光从玻璃板下表面斜向上射出,变成a、b两束单色光,如图所示.对于a、b两束光,下面说法正确的是( )
平行厚玻璃板放在空气中,一束复色光从玻璃板下表面斜向上射出,变成a、b两束单色光,如图所示.对于a、b两束光,下面说法正确的是( )| A. | 玻璃对a光的折射率较小 | B. | a光在玻璃中的传播速度较小 | ||
| C. | a光的波长较长 | D. | a光光子的能量较小 |
3.连接在电池两极上的平行板电容器,下极板固定并接地,当将上极板下移一些时,下列判断正确的是( )


| A. | 电容器的电容C变小 | |
| B. | 电容器极板的带电量Q变小 | |
| C. | 电容器两极板间的一点P的电势φ降低 | |
| D. | 电容器两极板间的电场强度E变小 |
 如图示的皮带传动装置,主动轮A,从动轮B,E是A轮上的一点,则E、C两点具有相同的角速度,C、D两点具有相同的线速度(选填”角速度”,”线速度”)
如图示的皮带传动装置,主动轮A,从动轮B,E是A轮上的一点,则E、C两点具有相同的角速度,C、D两点具有相同的线速度(选填”角速度”,”线速度”)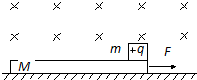 如图所示,光滑水平面上有一质量为M的足够长木板,板的右端放一质量为m、带正电荷量为q的绝缘滑块,滑块与板间的动摩擦因数为μ,在水平面上方有区域足够大的匀强磁场,磁感应强度大小为B、方向垂直纸面向里.开始时整个装置处于静止状态,现对木板施一水平向右的恒定拉力F=$\frac{1}{2}$μ(m+M)g,使其从静止开始向右运动,设滑块与木板间的最大静摩擦力等于两者间的滑动摩擦力.
如图所示,光滑水平面上有一质量为M的足够长木板,板的右端放一质量为m、带正电荷量为q的绝缘滑块,滑块与板间的动摩擦因数为μ,在水平面上方有区域足够大的匀强磁场,磁感应强度大小为B、方向垂直纸面向里.开始时整个装置处于静止状态,现对木板施一水平向右的恒定拉力F=$\frac{1}{2}$μ(m+M)g,使其从静止开始向右运动,设滑块与木板间的最大静摩擦力等于两者间的滑动摩擦力.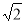 sin100πt V。若保持电压的有效值不变,只将电源频率改为25Hz,下列说法中正确的是
sin100πt V。若保持电压的有效值不变,只将电源频率改为25Hz,下列说法中正确的是