题目内容
 质量为M=9kg的小车A左端固定一根轻弹簧,车静止在光滑水平面上,一质量为m=1kg的小物块B从右端以速度v0=2m/s冲上小车并压缩弹簧,然后又被弹回,回到车右端时刚好与车保持相对静止.求全过程弹簧的最大弹性势能EP.
质量为M=9kg的小车A左端固定一根轻弹簧,车静止在光滑水平面上,一质量为m=1kg的小物块B从右端以速度v0=2m/s冲上小车并压缩弹簧,然后又被弹回,回到车右端时刚好与车保持相对静止.求全过程弹簧的最大弹性势能EP.分析:分别研究B从右端运动到弹簧压缩到最短的过程和从初状态到B又回到右端刚好相对静止的过程,由动量和能量关系列出等式求解.
解答:解:过程1:物块B从右端运动到弹簧压缩到最短的过程.弹簧压缩到最短时,A和B具有相同的速度v,
由动量和能量关系有:mv0=(m+M)v1
mv02=
(m+M)v12+Ep+μmgL
过程2:从初状态到m又回到右端刚好相对静止,A和B又具有相同的速度v2,
由动量和能量关系有:mv0=(m+M)v2
mv02=
(m+M)v22+2μmgL
联立以上四式,全过程弹簧的最大弹性势能EP=0.9J
答:全过程弹簧的最大弹性势能为0.9J.
由动量和能量关系有:mv0=(m+M)v1
| 1 |
| 2 |
| 1 |
| 2 |
过程2:从初状态到m又回到右端刚好相对静止,A和B又具有相同的速度v2,
由动量和能量关系有:mv0=(m+M)v2
| 1 |
| 2 |
| 1 |
| 2 |
联立以上四式,全过程弹簧的最大弹性势能EP=0.9J
答:全过程弹簧的最大弹性势能为0.9J.
点评:分析清楚物体运动过程是正确解题的关键,应用动量守恒定律与能量守恒定律即可正确解题.

练习册系列答案
相关题目
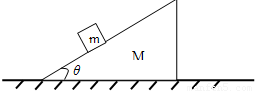
 如图所示,三角形木楔静置于粗糙水平地面上,木楔质量M=9kg、倾角θ=30°,三角形木楔的斜面上有一个质量为m=1kg的小物块.(重力加速度取g=10m/s2)
如图所示,三角形木楔静置于粗糙水平地面上,木楔质量M=9kg、倾角θ=30°,三角形木楔的斜面上有一个质量为m=1kg的小物块.(重力加速度取g=10m/s2)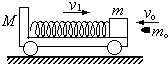 (1)下列说法正确的是
(1)下列说法正确的是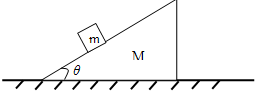 如图所示,三角形木楔静置于粗糙水平地面上,木楔质量M=9kg、倾角θ=30°,三角形木楔的斜面上有一个质量为m=1kg的小物块.(重力加速度取g=10m/s2)
如图所示,三角形木楔静置于粗糙水平地面上,木楔质量M=9kg、倾角θ=30°,三角形木楔的斜面上有一个质量为m=1kg的小物块.(重力加速度取g=10m/s2) ,有一个水平向左的恒力作用在木楔上,要使物块m相对斜面静止共同向左加速运动,求该水平恒力的大小.
,有一个水平向左的恒力作用在木楔上,要使物块m相对斜面静止共同向左加速运动,求该水平恒力的大小. ,有一个水平向左的恒力作用在木楔上,要使物块m相对斜面静止共同向左加速运动,求该水平恒力的大小.
,有一个水平向左的恒力作用在木楔上,要使物块m相对斜面静止共同向左加速运动,求该水平恒力的大小.