题目内容
7. 如图所示,水平面上有一物体,人通过定滑轮用绳子拉它,在图示位置时,若人的速度为$\sqrt{3}$m/s,则物体的瞬时速度为3m/s.
如图所示,水平面上有一物体,人通过定滑轮用绳子拉它,在图示位置时,若人的速度为$\sqrt{3}$m/s,则物体的瞬时速度为3m/s.
分析 将人和物体的速度沿绳子和垂直于绳子方向分解,抓住人和物体沿绳子方向的分速度相等,求出物体的瞬时速度.
解答 解:将人和物体的速度沿绳子和垂直于绳子方向分解,
如图,有v2cos60°=v1cos30°.则v2=$\frac{{v}_{1}cos30°}{cos60°}$=3m/s.
故答案为:3.
点评 解决本题的关键会运用平行四边形定则对速度进行分解,知道人和物体沿绳子方向的分速度相等.

练习册系列答案
 智慧课堂密卷100分单元过关检测系列答案
智慧课堂密卷100分单元过关检测系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案
相关题目
15.如图是某物体做直线运动的速度图象,由图象可得到的正确结果是( )


| A. | t=1s时物体的加速度大小为1.0m/s2 | |
| B. | t=5s时物体的加速度大小为0.75m/s2 | |
| C. | 第3s内物体的位移为1.5m | |
| D. | 物体在加速过程的速度变化率比减速过程的速度变化率大 |
12. 如图所示,竖直平面内光滑圆轨道半径R=2m,从最低点A有一质量为m=1kg的小球开始运动,初速度v0方向水平向右,重力加速度g取10m/s2,下列说法正确的是( )
如图所示,竖直平面内光滑圆轨道半径R=2m,从最低点A有一质量为m=1kg的小球开始运动,初速度v0方向水平向右,重力加速度g取10m/s2,下列说法正确的是( )
 如图所示,竖直平面内光滑圆轨道半径R=2m,从最低点A有一质量为m=1kg的小球开始运动,初速度v0方向水平向右,重力加速度g取10m/s2,下列说法正确的是( )
如图所示,竖直平面内光滑圆轨道半径R=2m,从最低点A有一质量为m=1kg的小球开始运动,初速度v0方向水平向右,重力加速度g取10m/s2,下列说法正确的是( )| A. | 小球能到达最高点B的条件是v0≥4$\sqrt{5}$m/s | |
| B. | 若初速度v0=5m/s,则运动过程中,小球一定不会脱离圆轨道 | |
| C. | 若初速度v0=8m/s,则小球将在离A点3.2m高的位置离开圆轨道 | |
| D. | 若初速度v0=8m/s,则小球离开圆轨道时的速度大小为2$\sqrt{2}$m/s |
19.甲 乙两车同时同地同向运动,甲车初速度为30m/s,以加速度大小为a1匀减速刹车,乙车初速度为10m/s,以加速度a2匀加速运动,经过时间t后两车速度共同速度为v.在乙车追上甲车之前两车之间最大距离为x.则( )
| A. | a1越大x越大 | B. | a2越小v越大 | C. | a1越大x越小 | D. | a2越大t越小 |
16.下列说法正确的是( )
| A. | 各种机械铭牌上所标的功率一般是额定功率 | |
| B. | 功率是标量,大小等于力和速度大小的乘积 | |
| C. | 力做功越多,力的功率就越大 | |
| D. | 汽车以一恒定的加速度从静止开始做匀加速运动的最长时间为t,此后开始以最大速度匀速运动 |
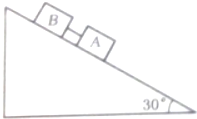 在一倾角为30°的斜面上有两个连接在一起的箱子A和B,质量分别为2kg和3kg,A和B斜面的摩擦系数分别为μA=0.1,μB=0.2,如图所示,试求物体AB的加速度.(取g=10m/s2)
在一倾角为30°的斜面上有两个连接在一起的箱子A和B,质量分别为2kg和3kg,A和B斜面的摩擦系数分别为μA=0.1,μB=0.2,如图所示,试求物体AB的加速度.(取g=10m/s2)
