题目内容
【题目】如图所示，静止在粗糙水平面上的A、B两个物体用水平轻绳相连，在水平力F作用下一起向右运动，当F增大到某一值F0时轻绳刚好被拉断，此时两物体的速度为v=2 m/s，此后水平力F0保持不变。已知轻绳能承受的最大拉力T=8 N，A的质量mA=2 kg，B的质量mB=8 kg，A、B物体与水平面间的动摩擦因数均为μ=0.2，重力加速度g取10 m/s2。求：
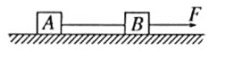
（1）F0的大小；
（2）物体A停止运动瞬间，B的速度大小。
【答案】（1）F0 = 40N （2）5m/s
【解析】
绳刚要被拉断时对分别A物体和对A、B整体，根据牛顿第二定律求出F0的大小；绳断后，根据牛顿第二定律求出A的加速度大小和B的加速度大小，根据运动学公式求出物体A停止运动瞬间，B的速度大小；
解：(1)绳刚要被拉断时根据牛顿第二定律，
对A物体有：
代入数据得：
对A、B整体：
代入数据得：
(2)设绳断后，A的加速度大小为aA，B的加速度大小为aB，则：
A物体停止运动时间tA ，则有：
则此时B加速到速度vB ，则有：
练习册系列答案
相关题目
