题目内容
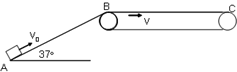 如图所示,一物体以初速度v0=10m/s冲上长度为SAB=3.2m的粗糙斜面,斜面与水平面的夹角θ=37°,斜面的末端B与传送带用光滑弧形相接,假设物体滑到B以后速度大小不变,方向马上变为水平向右,传送带始终保持v=2m/s的速率顺时针运行.已知传送带长度SBC=5m,物体与斜面及传送带间的动摩擦因数均为μ=0.5.试求:(其中g=10m/s2,sin37°=0.6,cos37°=0.8)
如图所示,一物体以初速度v0=10m/s冲上长度为SAB=3.2m的粗糙斜面,斜面与水平面的夹角θ=37°,斜面的末端B与传送带用光滑弧形相接,假设物体滑到B以后速度大小不变,方向马上变为水平向右,传送带始终保持v=2m/s的速率顺时针运行.已知传送带长度SBC=5m,物体与斜面及传送带间的动摩擦因数均为μ=0.5.试求:(其中g=10m/s2,sin37°=0.6,cos37°=0.8)(1)物体滑到斜面顶端B点时的速度vB的大小?
(2)物体从斜面底端A运动到传送带末端C所用的总时间t为多少?
分析:(1)根据牛顿第二定律求出物体在斜面上上滑的加速度,结合速度位移公式求出物体滑到斜面顶端的速度.
(2)根据速度时间公式求出物体从A到B的时间,滑块滑上传送带后先做匀减速直线运动,当速度达到传送带速度后一起做匀速直线运动,结合牛顿第二定律和运动学公式求出在传送带上的运行时间,从而得出整个过程的运行时间.
(2)根据速度时间公式求出物体从A到B的时间,滑块滑上传送带后先做匀减速直线运动,当速度达到传送带速度后一起做匀速直线运动,结合牛顿第二定律和运动学公式求出在传送带上的运行时间,从而得出整个过程的运行时间.
解答: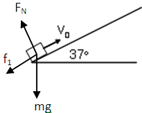 解:(1)物体在斜面上受力如图
解:(1)物体在斜面上受力如图
垂直于斜面有FN=mgcosθ
沿斜面方向有 mgsinθ+f1=ma1
又 f1=μFN
解a1=
=gsinθ+μgcosθ=(10×0.6+0.5×10×0.8)m/s2=10m/s2,方向沿斜面向下
由
-
=2as代入数据有:
-102=2×(-10)×3.2
解得物体运动到斜面顶点B的速度大小:vB=6m/s
(2)物体从A运动到B的时间:t1=
=
s=0.4s
物体从B开始向C运动时,相对传送带向右运动,受向左摩擦力,物体向右做匀减速直线运动,假设物体最后能与传送带速度相同.
物体做匀减速运动的加速度大小:a2=
=μg=0.5×10m/s2=5m/s2
匀减速运动时间:t2=
=
s=0.8s
匀减速运动通过的位移:s=
×t2=
×0.8m=3.2m<5m
故物体能与传送带同速,最后做匀速运动到达C点.
匀速运动的时间为t3=
=
=0.9s
从A运动到C的总时间:t=t1+t2+t3=2.1s.
答:(1)物体滑到斜面顶端B点时的速度vB的大小为6m/s.(2)物体从斜面底端A运动到传送带末端C所用的总时间t为2.1s.
 解:(1)物体在斜面上受力如图
解:(1)物体在斜面上受力如图垂直于斜面有FN=mgcosθ
沿斜面方向有 mgsinθ+f1=ma1
又 f1=μFN
解a1=
| mgsinθ+f1 |
| m |
由
| v | 2 t |
| v | 2 0 |
| v | 2 B |
解得物体运动到斜面顶点B的速度大小:vB=6m/s
(2)物体从A运动到B的时间:t1=
| vB-vA |
| -a1 |
| 6-10 |
| -10 |
物体从B开始向C运动时,相对传送带向右运动,受向左摩擦力,物体向右做匀减速直线运动,假设物体最后能与传送带速度相同.
物体做匀减速运动的加速度大小:a2=
| μmg |
| m |
匀减速运动时间:t2=
| v-vB |
| -a2 |
| 2-6 |
| -5 |
匀减速运动通过的位移:s=
| v+vB |
| 2 |
| 2+6 |
| 2 |
故物体能与传送带同速,最后做匀速运动到达C点.
匀速运动的时间为t3=
| sBC-s |
| v |
| 5-3.2 |
| 2 |
从A运动到C的总时间:t=t1+t2+t3=2.1s.
答:(1)物体滑到斜面顶端B点时的速度vB的大小为6m/s.(2)物体从斜面底端A运动到传送带末端C所用的总时间t为2.1s.
点评:解决本题的关键理清物体在整个过程中的运动规律,尤其在传送带上的运动过程分析,是一个难点,关键确定出摩擦力的方向,从而得出加速度的方向,得出物体的运动规律,知道物体速度与传送带速度相等后,一起做匀速直线运动.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 (2010?临渭区模拟)如图所示,一物体以初速度v0冲向光滑斜面AB,并能沿斜面升高h,下列说法中正确的是( )
(2010?临渭区模拟)如图所示,一物体以初速度v0冲向光滑斜面AB,并能沿斜面升高h,下列说法中正确的是( ) 如图所示,一物体以初速度v0冲上光滑的足够长斜面AB能沿斜面升高h,不计空气阻力.则下列说法中正确的是( )
如图所示,一物体以初速度v0冲上光滑的足够长斜面AB能沿斜面升高h,不计空气阻力.则下列说法中正确的是( ) 如图所示,一物体以初速度v0冲上光滑斜面AB,并恰好能沿斜面升高h,不计空气阻力,则下列说法中正确的是 ( )
如图所示,一物体以初速度v0冲上光滑斜面AB,并恰好能沿斜面升高h,不计空气阻力,则下列说法中正确的是 ( ) 如图所示,一物体以初速度v0冲向光滑斜面AB,并恰好能沿斜面升高h,下列说法中正确的是( )
如图所示,一物体以初速度v0冲向光滑斜面AB,并恰好能沿斜面升高h,下列说法中正确的是( )