题目内容
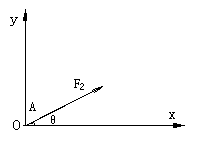
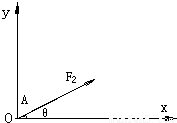
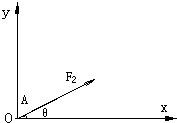如图所示是建立在光滑水平面上的直角坐标系，其原点O处放一个质量为m=2kg的物体，某时刻受到一个与x轴成370角的水平拉力F2=10N的作用，为了使物体能沿着X轴正方向运动，同时需要再一个水平方向的力F1的作用（已知sin37°=0.6 cos37°=0.8）．
问：
（1）F1的最小值为多少？如果物体在力F2和F1最小值的作用下从静止开始运动，5秒内的位移是多少？
（2）如果物体在力F2和F1最小值的作用下从静止开始运动，在5秒末的瞬间撤去F2，然后物体再运动5秒，求10秒末物体的速度．
解：（1）根据平等四边形法则得：F1=F2 sin37°=6N
物体所受的合外力为：F=F2 cos37°=8N
由牛顿第二定律F=ma，得a=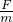
=4m/s2
由s=
=50m
故F1的最小值为6N，5秒内的位移是50m．
（2）当拉力F2撤去后，只在F1的作用下物体做类平抛运动
物体在x轴方向做匀速运动，在5秒末的速度为vx=at=20 m/s，
在y轴方向做匀加速直线运动，其加速度a=
=3 m/s2，vy=at=15
由此可知10秒末物体的速度：vt2=vx2+vy2，得vt=25 m/s
设物体的速度方向与x轴成θ角，则tanθ=
．
故10秒末物体的速度为25m/s．
分析：（1）已知F2的大小和方向，以及合力的方向，根据平行四边形定则，当F1的方向与x轴垂直时，F1最小．求出合力大小，根据牛顿第二定律求出加速度，再根据匀变速直线运动的位移时间公式s=求出位移．
（2）当拉力F2撤去后，只在F1的作用下物体做类平抛运动，在x轴方向做匀速直线运动，在在y轴方向做匀加速直线运动求出10s末在两个方向上的分速度，根据运动的合成求出物体的速度．
点评：解决本题的关键会根据一分力的大小和方向以及合力的方向求另一个分力的最小值．以及知道当拉力F2撤去后，只在F1的作用下物体做类平抛运动．
物体所受的合外力为：F=F2 cos37°=8N
由牛顿第二定律F=ma，得a=
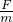=4m/s2由s=
=50m 故F1的最小值为6N，5秒内的位移是50m．
（2）当拉力F2撤去后，只在F1的作用下物体做类平抛运动
物体在x轴方向做匀速运动，在5秒末的速度为vx=at=20 m/s，
在y轴方向做匀加速直线运动，其加速度a=
=3 m/s2，vy=at=15 由此可知10秒末物体的速度：vt2=vx2+vy2，得vt=25 m/s
设物体的速度方向与x轴成θ角，则tanθ=
．故10秒末物体的速度为25m/s．
分析：（1）已知F2的大小和方向，以及合力的方向，根据平行四边形定则，当F1的方向与x轴垂直时，F1最小．求出合力大小，根据牛顿第二定律求出加速度，再根据匀变速直线运动的位移时间公式s=
求出位移．（2）当拉力F2撤去后，只在F1的作用下物体做类平抛运动，在x轴方向做匀速直线运动，在在y轴方向做匀加速直线运动求出10s末在两个方向上的分速度，根据运动的合成求出物体的速度．
点评：解决本题的关键会根据一分力的大小和方向以及合力的方向求另一个分力的最小值．以及知道当拉力F2撤去后，只在F1的作用下物体做类平抛运动．
练习册系列答案
相关题目
（2011?兴宁区模拟）在水平光滑的绝缘桌面内建立如图所示的直角坐标系，将第Ⅰ、Ⅱ象限称为区域一，第Ⅲ、Ⅳ象限称为区域二，其中一个区域内只有匀强电场，另一个区域内只有大小为2×10-2T、方向垂直桌面的匀强磁场．把一个荷质比为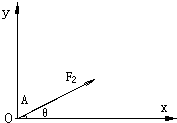
（2011?广东模拟）如图所示是建立在光滑水平面上的直角坐标系，其原点O处放一个质量为m=2kg的物体，某时刻受到一个与x轴成370角的水平拉力F2=10N的作用，为了使物体能沿着X轴正方向运动，同时需要再一个水平方向的力F1的作用（已知sin37°=0.6 cos37°=0.8）．
