题目内容
18.一个放在桌面上的木块,质量是0.10kg,在水平方向上受到0.06N的力,木块和桌面之间的动摩擦因数是0.02,求木块从静止开始通过1.8m所用的时间.分析 由牛顿第二定律求出加速度,然后由匀变速直线运动的位移公式求出木块的运动时间.
解答 解:由牛顿第二定律得:F-μmg=ma,
解得:a=$\frac{F}{m}$-μg=$\frac{0.06}{0.1}$-0.02×10=0.4m/s2,
木块做初速度为零的匀加速直线运动,
由匀变速直线运动的位移公式可知,
木块的运动时间:t=$\sqrt{\frac{2x}{a}}$=$\sqrt{\frac{2×1.8}{0.4}}$=3s;
答:木块从静止开始通过1.8m所用的时间是3s.
点评 本题考查了求木块的运动时间,分析清楚木块的运动过程、知道木块的运动性质是解题的关键,应用牛顿第二定律与运动学公式可以解题.

练习册系列答案
相关题目
3.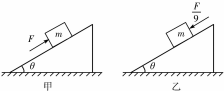 一斜面体固定在水平面上,斜面的倾角为θ,物体的质量为m,如图甲所示,在沿斜面向上的力F作用下,物体沿斜面向上做匀速运动;如图乙所示,在沿斜面向下的力$\frac{F}{9}$作用下,物体沿斜面向下做匀速运动,则物体与斜面间的动摩擦因数为( )
一斜面体固定在水平面上,斜面的倾角为θ,物体的质量为m,如图甲所示,在沿斜面向上的力F作用下,物体沿斜面向上做匀速运动;如图乙所示,在沿斜面向下的力$\frac{F}{9}$作用下,物体沿斜面向下做匀速运动,则物体与斜面间的动摩擦因数为( )
 一斜面体固定在水平面上,斜面的倾角为θ,物体的质量为m,如图甲所示,在沿斜面向上的力F作用下,物体沿斜面向上做匀速运动;如图乙所示,在沿斜面向下的力$\frac{F}{9}$作用下,物体沿斜面向下做匀速运动,则物体与斜面间的动摩擦因数为( )
一斜面体固定在水平面上,斜面的倾角为θ,物体的质量为m,如图甲所示,在沿斜面向上的力F作用下,物体沿斜面向上做匀速运动;如图乙所示,在沿斜面向下的力$\frac{F}{9}$作用下,物体沿斜面向下做匀速运动,则物体与斜面间的动摩擦因数为( )| A. | $\frac{5}{4}$cotθ | B. | $\frac{4}{5}$cotθ | C. | $\frac{5}{4}$tanθ | D. | $\frac{4}{5}$tanθ |
8.下列说法中正确的是( )
| A. | 通过导线横截面的电量越多,电流越大 | |
| B. | 有恒定电流通过的导体内部的电场强度为零 | |
| C. | 单位时间内通过导体横截面的电量越多,导体中的电流越大 | |
| D. | 通电导线中自由电子定向移动的速率等于电流的传导速率 |
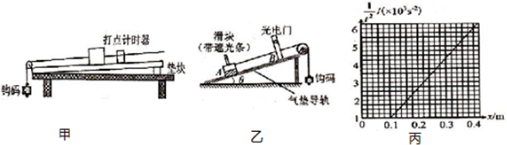
 如图所示,用F=2.0N的水平拉力,使质量m=2.0kg的物体由静止开始沿光滑水平面做匀加速直线运动.求:
如图所示,用F=2.0N的水平拉力,使质量m=2.0kg的物体由静止开始沿光滑水平面做匀加速直线运动.求: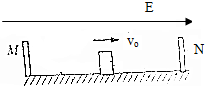 如图所示,在粗糙水平面上相距L=1.0m处,固定有两个绝缘挡板M,N,在它们正中间有一个质量为m=5.0×10-2kg,电荷量为q=-2.0×10-4C的带电物体A(可视为质点),A与水平面间的动摩擦因数μ=0.10,空间有水平向右的匀强电场,场强E=2.5×102V/m.取g=10m/s2,现给A一个初速度v0=3.0m/s向右运动,设A与挡板M,N碰撞过程没有动能损失.求:
如图所示,在粗糙水平面上相距L=1.0m处,固定有两个绝缘挡板M,N,在它们正中间有一个质量为m=5.0×10-2kg,电荷量为q=-2.0×10-4C的带电物体A(可视为质点),A与水平面间的动摩擦因数μ=0.10,空间有水平向右的匀强电场,场强E=2.5×102V/m.取g=10m/s2,现给A一个初速度v0=3.0m/s向右运动,设A与挡板M,N碰撞过程没有动能损失.求: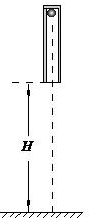 如图所示,一个质量为M的长圆管竖直放置,顶端塞有一个质量为m的弹性小球,M=4m,球和管间的滑动摩擦力和最大静摩擦力大小均为4mg,管从下端离地面距离为H处自由落下,运动过程中,管始终保持竖直,每次落地后向上弹起的速度与落地时速度大小相等,不计空气阻力,重力加速度为g.求:
如图所示,一个质量为M的长圆管竖直放置,顶端塞有一个质量为m的弹性小球,M=4m,球和管间的滑动摩擦力和最大静摩擦力大小均为4mg,管从下端离地面距离为H处自由落下,运动过程中,管始终保持竖直,每次落地后向上弹起的速度与落地时速度大小相等,不计空气阻力,重力加速度为g.求: 火箭内的实验平台有质量为18㎏的测试仪器,火箭从地面起动后以加速度a=$\frac{g}{2}$竖直匀加速上升,g=10m/s2试求:
火箭内的实验平台有质量为18㎏的测试仪器,火箭从地面起动后以加速度a=$\frac{g}{2}$竖直匀加速上升,g=10m/s2试求: 如图所示,有一光滑斜面,斜面的长度为8m,在斜面底端A处有一质量为1kg的小物体,正在以沿斜面向上的初速度v0=10m/s开始向上滑动,已知物体沿斜面滑动时具有沿斜面向下的大小为5m/s2的加速度,求物体到达离顶端0.5m的B处要经过多长时间?
如图所示,有一光滑斜面,斜面的长度为8m,在斜面底端A处有一质量为1kg的小物体,正在以沿斜面向上的初速度v0=10m/s开始向上滑动,已知物体沿斜面滑动时具有沿斜面向下的大小为5m/s2的加速度,求物体到达离顶端0.5m的B处要经过多长时间?