题目内容
9.在图示装置中,两个光滑定滑轮的半径很小,表面粗糙的斜面固定在地面上,倾角为θ=30°.用一根跨过定滑轮的轻绳连接甲、乙两物体,甲物体放在斜面上且绳与斜面平行,乙物体悬在空中,并使悬线拉直且偏离竖直方向α=60°,现同时释放甲、乙两物体,乙将在竖直平面内摆动,当乙经过最高点和最低点时,甲在斜面上均恰好未滑动.已知乙的质量为m=1Kg,取g=10m/s2,试求:
(1)乙经过最高点和最低点时悬绳的拉力大小?
(2)甲的质量及斜面对甲物体的最大静摩擦力?
分析 乙物体摆到最高点时绳子拉力最小,根据沿绳子方向合力为零求出绳子的拉力;摆到最低点时绳子拉力最大,根据动能定理结合牛顿第二定律求出乙物体在最低点时绳子的拉力.当绳子的拉力最小时,甲物体有沿斜面向上的最大静摩擦力,当绳子拉力最大时,甲物体有沿斜面向下的最大静摩擦力,根据共点力平衡求出甲物体的质量和斜面对甲物体的最大静摩擦力
解答 解:(1)乙物体摆到最高点时绳子拉力最小,有:m乙gcos60°=T1=5N.
由最高点到最低点,根据动能定理得:$mgl(1-cos60°)=\frac{1}{2}m{v}^{2}$,
根据牛顿第二定律得:${T}_{2}-mg=m\frac{{v}^{2}}{l}$.
联立两式得,T2=20N.
(2)对甲物体有:m甲gsin30°=T1+fm,
m甲gsin30°+fm=T2,
联立两式得:
m甲=2.5kg,fm=7.5N.
答:(1)乙经过最高点时绳子的拉力为5N,最低点时悬绳的拉力为20N;
(2)甲的质量为2.5Kg,斜面对甲物体的最大静摩擦力为7.5N.
点评 解决本题的关键知道乙物体摆到最低点时有最大拉力,摆到最高点时有最小拉力.以及知道在乙物体摆到最低点时有沿斜面向下的最大静摩擦力,摆到最高点时有沿斜面向上的最大静摩擦力

练习册系列答案
 孟建平名校考卷系列答案
孟建平名校考卷系列答案
相关题目
1.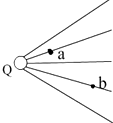 如图所示,实线是一簇未标明方向的由点电荷Q产生的电场线,若带电粒子q(|Q|>>q)由a运动到b,电场力做正功,已知在a、b两点粒子所受电场力分别为Fa、Fb,则下例判断正确的是( )
如图所示,实线是一簇未标明方向的由点电荷Q产生的电场线,若带电粒子q(|Q|>>q)由a运动到b,电场力做正功,已知在a、b两点粒子所受电场力分别为Fa、Fb,则下例判断正确的是( )
 如图所示,实线是一簇未标明方向的由点电荷Q产生的电场线,若带电粒子q(|Q|>>q)由a运动到b,电场力做正功,已知在a、b两点粒子所受电场力分别为Fa、Fb,则下例判断正确的是( )
如图所示,实线是一簇未标明方向的由点电荷Q产生的电场线,若带电粒子q(|Q|>>q)由a运动到b,电场力做正功,已知在a、b两点粒子所受电场力分别为Fa、Fb,则下例判断正确的是( )| A. | 若Q为正电荷,则q带正电,Fa>Fb | B. | 若Q为正电荷,则q带正电,Fa<Fb | ||
| C. | 若Q为负电荷,则q带正电,Fa>Fb | D. | 若Q为负电荷,则q带正电,Fa<Fb |
20.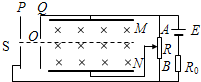 如图所示,相距为d的水平金属板M、N的左侧有一对竖直金属板P、Q,板P上的小孔S正对板Q上的小孔O.M、N间有垂直纸面向里的匀强磁场,在小孔S处有一带电的负粒子,其重力和初速不计.当变阻器的滑动触头在AB的中点时,粒子恰能在M、N间做直线运动.当滑动变阻器滑片滑到A点后,则( )
如图所示,相距为d的水平金属板M、N的左侧有一对竖直金属板P、Q,板P上的小孔S正对板Q上的小孔O.M、N间有垂直纸面向里的匀强磁场,在小孔S处有一带电的负粒子,其重力和初速不计.当变阻器的滑动触头在AB的中点时,粒子恰能在M、N间做直线运动.当滑动变阻器滑片滑到A点后,则( )
 如图所示,相距为d的水平金属板M、N的左侧有一对竖直金属板P、Q,板P上的小孔S正对板Q上的小孔O.M、N间有垂直纸面向里的匀强磁场,在小孔S处有一带电的负粒子,其重力和初速不计.当变阻器的滑动触头在AB的中点时,粒子恰能在M、N间做直线运动.当滑动变阻器滑片滑到A点后,则( )
如图所示,相距为d的水平金属板M、N的左侧有一对竖直金属板P、Q,板P上的小孔S正对板Q上的小孔O.M、N间有垂直纸面向里的匀强磁场,在小孔S处有一带电的负粒子,其重力和初速不计.当变阻器的滑动触头在AB的中点时,粒子恰能在M、N间做直线运动.当滑动变阻器滑片滑到A点后,则( )| A. | 粒子在M、N间运动的过程中.动能将减小 | |
| B. | 粒子在M、N间运动的过程中,动能将增大 | |
| C. | 粒子在M、N间将做圆周运动 | |
| D. | 粒于在M、N间运动的过程中,电势能将不断增大 |
17.根据分子动理论,设两个分子间的距离为r0时分子间的引力和斥力相等,当两分子间距离r>r0时,增大r,以下说法正确的是( )
| A. | 分子间的引力、斥力均减小,分子力表现为引力,分子势能增大 | |
| B. | 分子间的引力、斥力均增大,而分子力表现为引力,分子势能减小 | |
| C. | 分子间的引力、斥力均增大,而分子力表现为斥力,分子势能增大 | |
| D. | 分子间的引力、斥力均减小,而分子力表现为斥力,分子势能减小 |
4. 2008年9月25日21点10分,酒泉卫星发射中心用长征二号F火箭将神舟七号飞船发射升空,飞船最后在距地高度为343公里的圆轨道上运动;2010年11月1日零时26分,西昌卫星发射中心用“长征三号丙”运载火箭,将第六颗北斗导航卫星成功送人太空,它是一颗地球同步轨道卫星.下列关于第六颗北斗导航卫星与神舟七号飞船的说法正确的是( )
2008年9月25日21点10分,酒泉卫星发射中心用长征二号F火箭将神舟七号飞船发射升空,飞船最后在距地高度为343公里的圆轨道上运动;2010年11月1日零时26分,西昌卫星发射中心用“长征三号丙”运载火箭,将第六颗北斗导航卫星成功送人太空,它是一颗地球同步轨道卫星.下列关于第六颗北斗导航卫星与神舟七号飞船的说法正确的是( )
 2008年9月25日21点10分,酒泉卫星发射中心用长征二号F火箭将神舟七号飞船发射升空,飞船最后在距地高度为343公里的圆轨道上运动;2010年11月1日零时26分,西昌卫星发射中心用“长征三号丙”运载火箭,将第六颗北斗导航卫星成功送人太空,它是一颗地球同步轨道卫星.下列关于第六颗北斗导航卫星与神舟七号飞船的说法正确的是( )
2008年9月25日21点10分,酒泉卫星发射中心用长征二号F火箭将神舟七号飞船发射升空,飞船最后在距地高度为343公里的圆轨道上运动;2010年11月1日零时26分,西昌卫星发射中心用“长征三号丙”运载火箭,将第六颗北斗导航卫星成功送人太空,它是一颗地球同步轨道卫星.下列关于第六颗北斗导航卫星与神舟七号飞船的说法正确的是( )| A. | 北斗导航卫星的运行周期小于“神州七号” | |
| B. | 北斗导航卫星的轨道半径大于“神州七号” | |
| C. | 北斗导航卫星的角速度与其质量有关 | |
| D. | 北斗导航卫星的线速度与其质量有关 |
14. 如图所示,A和B是两根竖直立在地上的木桩,轻绳系在两木桩上不等高的P和Q两点,C为光滑的、质量不计的滑轮,下面悬挂这重物G,现保持结点P的位置不变,当Q点的位置变化时,轻绳的张力大小变化情况是( )
如图所示,A和B是两根竖直立在地上的木桩,轻绳系在两木桩上不等高的P和Q两点,C为光滑的、质量不计的滑轮,下面悬挂这重物G,现保持结点P的位置不变,当Q点的位置变化时,轻绳的张力大小变化情况是( )
 如图所示,A和B是两根竖直立在地上的木桩,轻绳系在两木桩上不等高的P和Q两点,C为光滑的、质量不计的滑轮,下面悬挂这重物G,现保持结点P的位置不变,当Q点的位置变化时,轻绳的张力大小变化情况是( )
如图所示,A和B是两根竖直立在地上的木桩,轻绳系在两木桩上不等高的P和Q两点,C为光滑的、质量不计的滑轮,下面悬挂这重物G,现保持结点P的位置不变,当Q点的位置变化时,轻绳的张力大小变化情况是( )| A. | Q点上下移动时,张力不变 | B. | Q点向上移动时,张力变大 | ||
| C. | Q点向下移动时,张力变小 | D. | 条件不足,无法判断 |
1.对于自由落体运动,下列说法正确的是(g=10m/s2)( )
| A. | 在1s内、2s内、3s内的位移之比是1:4:9 | |
| B. | 在1s末、2s末、3s末的速度之比是1:3:5 | |
| C. | 在第1s内、第2s内、第3s内的平均速度之比是1:3:5 | |
| D. | 在任意相邻两个1s内的位移之差都是10m |
18. 某家用桶装纯净水手压式饮水器如图所示,在手连续稳定的按压下,出水速度为V,供水系统机械效率为η,现测量出桶底到出水管之间的高度差H,桶中水面到出水管之间的高度差是h,出水口倾斜,离出水管的高度差可忽略,出水口的横截面积为S,水的密度为ρ,重力加速度为g,则下列说法正确的是( )
某家用桶装纯净水手压式饮水器如图所示,在手连续稳定的按压下,出水速度为V,供水系统机械效率为η,现测量出桶底到出水管之间的高度差H,桶中水面到出水管之间的高度差是h,出水口倾斜,离出水管的高度差可忽略,出水口的横截面积为S,水的密度为ρ,重力加速度为g,则下列说法正确的是( )
 某家用桶装纯净水手压式饮水器如图所示,在手连续稳定的按压下,出水速度为V,供水系统机械效率为η,现测量出桶底到出水管之间的高度差H,桶中水面到出水管之间的高度差是h,出水口倾斜,离出水管的高度差可忽略,出水口的横截面积为S,水的密度为ρ,重力加速度为g,则下列说法正确的是( )
某家用桶装纯净水手压式饮水器如图所示,在手连续稳定的按压下,出水速度为V,供水系统机械效率为η,现测量出桶底到出水管之间的高度差H,桶中水面到出水管之间的高度差是h,出水口倾斜,离出水管的高度差可忽略,出水口的横截面积为S,水的密度为ρ,重力加速度为g,则下列说法正确的是( )| A. | 出水口单位时间内的出水体积Q=VS | |
| B. | 出水口所出水落地时的速度$\sqrt{2gH}$ | |
| C. | 出水后,手连续稳定按压的功率为$\frac{{ρS{V^3}}}{2η}+\frac{ρVSgh}{η}$ | |
| D. | 手按压输入的功率等于单位时间内所出水的动能和重力势能之和 |
19.某物体运动的位移-时间图象如图所示,则物体( )


| A. | 往复运动 | B. | 匀速直线运动 | ||
| C. | 朝某一方向直线运动 | D. | 匀加速直线运动 |