题目内容
如图所示,在光滑的桌面上叠放着质量mA=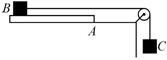
3.8 s
解析:设经时间t剪断轻线,剪断线前:A的加速度为a1,对地位移为s1,B的加速度为a2,对地位移为s2,则:
ΜmBg=maa1 mcg-μmBg=(mB+mC)a2
s1=![]() a1t2 s2=
a1t2 s2=![]() a2t2
a2t2
剪断轻线时,A的速度v1=a1t B的速度v2=a2t
剪断轻线后,A、B组成的系统动量守恒,设B恰好能到达A的右端时A、B的共同速度为,则:
mAv1+mBv2=(mA+mB)v
μmBg[l-(s2-s1)]=![]() +
+![]() -
-![]() (mA+mB)v2
(mA+mB)v2
解得:t=![]() s=3.8 s
s=3.8 s
即B要能从A的右端滑下,至少要经过3.8 s才允许剪断轻线。

练习册系列答案
 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案
相关题目
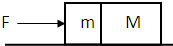 如图所示,在光滑的桌面上有M、m两个物块,现用力F推物块m,使M、m两物块在桌上一起向右加速,则M、m间的相互作用力为( )
如图所示,在光滑的桌面上有M、m两个物块,现用力F推物块m,使M、m两物块在桌上一起向右加速,则M、m间的相互作用力为( )| A、F | ||
B、
| ||
C、若桌面的摩擦因数为μ,M、m仍向右加速,则M、m间的相互作用力为
| ||
D、若桌面的摩擦因数为μ,M、m仍向右加速,则M、m间的相互作用力仍为
|
如图所示,在光滑的桌面上有M、m两个物块,现用力F推物块m,使M、m两物块在桌上一起向右加速,则M、m间的相互作用力为:( )
A. |
B. |
C.若桌面的摩擦因数为 ,M、m仍向右加速,则M、m间的相互作用力为 ,M、m仍向右加速,则M、m间的相互作用力为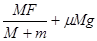 |
D.若桌面的摩擦因数为 ,M、m仍向右加速,则M、m间的相互作用力为 ,M、m仍向右加速,则M、m间的相互作用力为 |
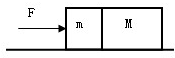 如图所示,在光滑的桌面上有M、m两个物块,现用力F推物块m,使M、m两物块在桌上一起向右加速,则M、m间的相互作用力为( )
如图所示,在光滑的桌面上有M、m两个物块,现用力F推物块m,使M、m两物块在桌上一起向右加速,则M、m间的相互作用力为( )


 ,M、m仍向右加速,则M、m间的相互作用力为
,M、m仍向右加速,则M、m间的相互作用力为
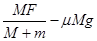



 ,M、m仍向右加速,则M、m间的相互作用力为
,M、m仍向右加速,则M、m间的相互作用力为