题目内容
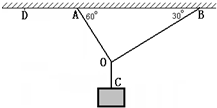
如图所示,三根轻质绳子OA、OB与OC将一质量为10kg的重物悬挂空中而处于静止状态,其中OB与天花板夹角为30°,OA与天花板夹角为60°,g取10m/s2)
(1)求绳子OA、OB对应的拉力大小FA、FB
(2)若保持0、B点位置不变,改变OA绳长度,将A点移动到D点,使得OD=OB,求此时绳子OD对应的拉力大小FD.
(1)求绳子OA、OB对应的拉力大小FA、FB
(2)若保持0、B点位置不变,改变OA绳长度,将A点移动到D点,使得OD=OB,求此时绳子OD对应的拉力大小FD.

(1)画出受力如图所示,根据平衡条件运用合成法,
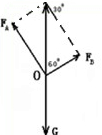
由几何知识得:FA=mgcos30°=50
N
FB=mgsin30°=50 N;
(2)将A点移动到D点后画出受力如图所示:
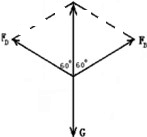
运用合成法,由几何知识得:
FD=mg=100N;
答:(1)绳子OA、OB对应的拉力大小FA、FB分别为50
N、50 N;
(2)将A点移动到D点,使得OD=OB,此时绳子OD对应的拉力大小为100N.

由几何知识得:FA=mgcos30°=50
| 3 |
FB=mgsin30°=50 N;
(2)将A点移动到D点后画出受力如图所示:

运用合成法,由几何知识得:
FD=mg=100N;
答:(1)绳子OA、OB对应的拉力大小FA、FB分别为50
| 3 |
(2)将A点移动到D点,使得OD=OB,此时绳子OD对应的拉力大小为100N.

练习册系列答案
相关题目