题目内容
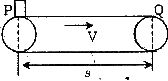
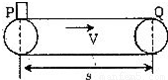
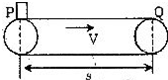 如图,某货场一水平的皮带运输机以速度v=2m/s匀速运动,把P处的物体运送到Q处,P、Q相距s=10m,在P处把物体无初速的放在皮带上,经时间t=6s传送到Q处,现欲用最短时间把物体从P处传送到Q处(传送皮带与物体间动摩擦因数不变),则传送皮带的运行速度至少应为多大?(保留两位有效数字)
如图,某货场一水平的皮带运输机以速度v=2m/s匀速运动,把P处的物体运送到Q处,P、Q相距s=10m,在P处把物体无初速的放在皮带上,经时间t=6s传送到Q处,现欲用最短时间把物体从P处传送到Q处(传送皮带与物体间动摩擦因数不变),则传送皮带的运行速度至少应为多大?(保留两位有效数字)
解:工件放到P端受传送带上,恒定的水平向右滑动摩擦力作用,先做匀加速运动,速度由O增大到v;再随传送带一起匀速运动到Q处.
工件匀加速度运动时间为t1,则有
s1=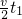
工件匀速运动时间为t2,位移s2=vt2
由题有:t1+t2=t,s1+s2=s
联立解得,t1=2s,t2=4s
又v=at1,得a=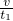
代入解得a=1m/s2
若提高传送带速率为v′>v时,工件加速运动所受滑动摩擦力不变,a不变,工件由P到Q一直处于匀加速运动时所用时间最短.
设最短时间为t′,则
L=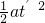
解得:t′=2 s
s
工件到Q时速度v′=at′=2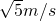
即传送带速率至少应等于4.5m/s.
答:传送皮带的运行速度至少4.5m/s.
分析:工件放到P端受传送的滑动摩擦力作用先做匀加速运动,后做匀速直线运动,根据牛顿第二定律求出加速度,再由运动学公式分别列出加速与匀速运动的位移,根据总位移等于皮带的长度求出加速度.若提高传送带速率,工件加速运动的加速度不变,工件由P到Q一直处于匀加速运动时所用时间最短,根据位移公式求出最短时间.
点评:本题物体放在传送带上,关键分析物体的运动情况,第(2)问也可以运用速度图象分析什么条件下时间最短.
工件匀加速度运动时间为t1,则有
s1=
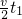
工件匀速运动时间为t2,位移s2=vt2
由题有:t1+t2=t,s1+s2=s
联立解得,t1=2s,t2=4s
又v=at1,得a=
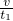
代入解得a=1m/s2
若提高传送带速率为v′>v时,工件加速运动所受滑动摩擦力不变,a不变,工件由P到Q一直处于匀加速运动时所用时间最短.
设最短时间为t′,则
L=
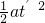
解得:t′=2
 s
s工件到Q时速度v′=at′=2
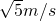
即传送带速率至少应等于4.5m/s.
答:传送皮带的运行速度至少4.5m/s.
分析:工件放到P端受传送的滑动摩擦力作用先做匀加速运动,后做匀速直线运动,根据牛顿第二定律求出加速度,再由运动学公式分别列出加速与匀速运动的位移,根据总位移等于皮带的长度求出加速度.若提高传送带速率,工件加速运动的加速度不变,工件由P到Q一直处于匀加速运动时所用时间最短,根据位移公式求出最短时间.
点评:本题物体放在传送带上,关键分析物体的运动情况,第(2)问也可以运用速度图象分析什么条件下时间最短.

练习册系列答案
相关题目
 (2007?漳州模拟)某货场两站台A、B之间的水平传送装置如图所示,两站台与传送带处于同一水平面,A、B之间的水平距离S0=4m(等于传送带的长度),传送带的运行速度v0=5m/s,方向如图,现将一质量m=10kg的货物自A端由静止开始运送到B端,求摩擦力对货物做功的平均功率?(已知货物与传送带之间的动摩擦因数μ=0.02,取g=10m/s2)
(2007?漳州模拟)某货场两站台A、B之间的水平传送装置如图所示,两站台与传送带处于同一水平面,A、B之间的水平距离S0=4m(等于传送带的长度),传送带的运行速度v0=5m/s,方向如图,现将一质量m=10kg的货物自A端由静止开始运送到B端,求摩擦力对货物做功的平均功率?(已知货物与传送带之间的动摩擦因数μ=0.02,取g=10m/s2)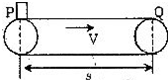 如图,某货场一水平的皮带运输机以速度v=2m/s匀速运动,把P处的物体运送到Q处,P、Q相距s=10m,在P处把物体无初速的放在皮带上,经时间t=6s传送到Q处,现欲用最短时间把物体从P处传送到Q处(传送皮带与物体间动摩擦因数不变),则传送皮带的运行速度至少应为多大?(保留两位有效数字)
如图,某货场一水平的皮带运输机以速度v=2m/s匀速运动,把P处的物体运送到Q处,P、Q相距s=10m,在P处把物体无初速的放在皮带上,经时间t=6s传送到Q处,现欲用最短时间把物体从P处传送到Q处(传送皮带与物体间动摩擦因数不变),则传送皮带的运行速度至少应为多大?(保留两位有效数字)