题目内容
4. 如图所示,一个圆环环心在O处,PO与直径AB夹角为60°,QO与直径AB夹角为30°,若以其直径AB为轴作匀速转动,则环上的P和Q两点的线速度之比是$\sqrt{3}:1$,若环的半径为20 cm.绕AB转动的周期是0.5s,则环上Q点的线速度为0.4πm/s.
如图所示,一个圆环环心在O处,PO与直径AB夹角为60°,QO与直径AB夹角为30°,若以其直径AB为轴作匀速转动,则环上的P和Q两点的线速度之比是$\sqrt{3}:1$,若环的半径为20 cm.绕AB转动的周期是0.5s,则环上Q点的线速度为0.4πm/s.
分析 同一圆环以直径为轴做匀速转动时,环上的点的角速度相同,根据几何关系可以求得Q、P两点各自做圆周运动的半径,根据v=ωr即可求解线速度之比;
根据$v=\frac{2πr}{T}$求得线速度
解答 解:P、Q两点以它的直径AB为轴做匀速转动,它们的角速度相同都为ω,
所以Q点转动的半径为:${r}_{1}=Rsin30°=\frac{1}{2}R$,
P点转动的半径为:${r}_{2}=Rsin60°=\frac{\sqrt{3}}{2}R$,
根据v=ωr得:$\frac{{v}_{P}}{{v}_{Q}}=\frac{{r}_{2}}{{r}_{1}}=\frac{\sqrt{3}}{1}$
根据$v=\frac{2πr}{T}$可得:
v=$\frac{2π{r}_{1}}{T}=\frac{2π×0.1}{0.5}m/s=0.4πm/s$
故答案为:$\sqrt{3}:1$,0.4π
点评 题主要考查了圆周运动基本公式的直接应用,注意同轴转动时角速度相同.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
14.平放在水平桌面上的线圈正上方有一竖直的条形磁铁,在条形磁铁竖直向下靠近线圈的过程中,穿过线圈的磁通量( )
| A. | 一直增大 | B. | 一直减小 | C. | 先增大后减小 | D. | 先减小后增大 |
15.若河水的流速大小与水到河岸的距离有关,河中心水的流速最大,河岸边缘处水的流速最小,现假设河的宽度为120m.河中心水的流速大小为4m/s,船在静水中的速度大小为 3m/s,则( )
| A. | 船渡河的最短时间是24 s | B. | 船可以垂直过河 | ||
| C. | 船在河水中航行的轨迹是一条直线 | D. | 船在河水中的最大速度为5 m/s |
12.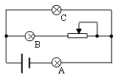 如图所示电路中,若滑动变阻器滑动触头向左移动时,电灯A、B、C的电流强度将(电灯的电阻不变)( )
如图所示电路中,若滑动变阻器滑动触头向左移动时,电灯A、B、C的电流强度将(电灯的电阻不变)( )
 如图所示电路中,若滑动变阻器滑动触头向左移动时,电灯A、B、C的电流强度将(电灯的电阻不变)( )
如图所示电路中,若滑动变阻器滑动触头向左移动时,电灯A、B、C的电流强度将(电灯的电阻不变)( )| A. | 都变大 | B. | 都变小 | C. | A、C变大,B变小 | D. | A、B变大,C变小 |
19.关于电场场强的概念,下列说法正确的是( )
| A. | 由 E=$\frac{F}{q}$可知,某电场的场强 E 与 q 成反比,与 F 成正比 | |
| B. | 正负试探电荷在同一点受到的电场力方向相反,所以某一点场强方向与试探电荷的正负有关 | |
| C. | 电场中某一点的场强与放入该点的试探电荷正负无关 | |
| D. | 电场中某一点不放试探电荷时,该点场强等于零 |
9.关于一列简谐波,下面说法中正确的是( )
| A. | 波动的产生需要两个条件,即波源和传播波的介质 | |
| B. | 波动过程是质点由近向远传递的过程 | |
| C. | 波由一种介质传到另一种介质进,频率变大 | |
| D. | 同一性质的波在同种介质中传递时,频率不同,波速不同 |
16.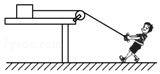 如图所示,光滑水平平台上有一个质量为m的物块,站在地面上的人用跨过定滑轮的绳子向右拉动物块,不计绳和滑轮的质量及滑轮的摩擦,且平台边缘离人手作用点竖直高度始终为h.当人以速度v从平台的边缘处向右匀速前进位移x时,则( )
如图所示,光滑水平平台上有一个质量为m的物块,站在地面上的人用跨过定滑轮的绳子向右拉动物块,不计绳和滑轮的质量及滑轮的摩擦,且平台边缘离人手作用点竖直高度始终为h.当人以速度v从平台的边缘处向右匀速前进位移x时,则( )
 如图所示,光滑水平平台上有一个质量为m的物块,站在地面上的人用跨过定滑轮的绳子向右拉动物块,不计绳和滑轮的质量及滑轮的摩擦,且平台边缘离人手作用点竖直高度始终为h.当人以速度v从平台的边缘处向右匀速前进位移x时,则( )
如图所示,光滑水平平台上有一个质量为m的物块,站在地面上的人用跨过定滑轮的绳子向右拉动物块,不计绳和滑轮的质量及滑轮的摩擦,且平台边缘离人手作用点竖直高度始终为h.当人以速度v从平台的边缘处向右匀速前进位移x时,则( )| A. | 在该过程中,物块做加速运动 | |
| B. | 在该过程中,人对物块做的功为$\frac{m{v}^{2}{x}^{2}}{2({h}^{2}+{x}^{2})}$ | |
| C. | 在该过程中,人对物块做的功为$\frac{1}{2}$mv2 | |
| D. | 人前进x时,物块的运动速率为$\frac{vx}{\sqrt{{x}^{2}+{h}^{2}}}$ |
14. 如图所示,质量均为m的A、B两球之间系着一条轻弹簧放在光滑的水平面上,A球靠紧墙壁,现用力F将B球向左推压弹簧,平衡后,突然将力F撤去的瞬间,则( )
如图所示,质量均为m的A、B两球之间系着一条轻弹簧放在光滑的水平面上,A球靠紧墙壁,现用力F将B球向左推压弹簧,平衡后,突然将力F撤去的瞬间,则( )
 如图所示,质量均为m的A、B两球之间系着一条轻弹簧放在光滑的水平面上,A球靠紧墙壁,现用力F将B球向左推压弹簧,平衡后,突然将力F撤去的瞬间,则( )
如图所示,质量均为m的A、B两球之间系着一条轻弹簧放在光滑的水平面上,A球靠紧墙壁,现用力F将B球向左推压弹簧,平衡后,突然将力F撤去的瞬间,则( )| A. | 突然将F撤去瞬间,两球的速度和加速度均为0 | |
| B. | A球离开墙壁后,两球的速度相等时弹簧恰好恢复原长 | |
| C. | B球运动过程中加速度的最大值为$\frac{F}{2m}$ | |
| D. | A球离开墙壁后,两球的加速度始终大小相等,方向相反 |
15.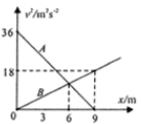 A、B两辆汽车从同一地点同时出发沿同一方向做直线运动,它们的速度的平方(v2)随位置(x)的变化图象如图所示,下列判断正确的是( )
A、B两辆汽车从同一地点同时出发沿同一方向做直线运动,它们的速度的平方(v2)随位置(x)的变化图象如图所示,下列判断正确的是( )
 A、B两辆汽车从同一地点同时出发沿同一方向做直线运动,它们的速度的平方(v2)随位置(x)的变化图象如图所示,下列判断正确的是( )
A、B两辆汽车从同一地点同时出发沿同一方向做直线运动,它们的速度的平方(v2)随位置(x)的变化图象如图所示,下列判断正确的是( )| A. | 汽车A的加速度大小为4m/s2 | |
| B. | 汽车A、B在x=6m处的速度大小为2$\sqrt{3}$m/s | |
| C. | 汽车A、B在x=8m处相遇 | |
| D. | 汽车A、B在x=9m处相遇 |