题目内容
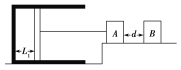
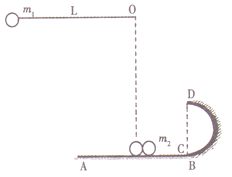
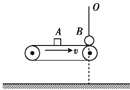
【题目】如图所示，一足够长的传送带以
的速度顺时针匀速运动，在
时刻，把质量
的小物块A由静止轻放在传送带中间位置，小物块与传送带间的动摩擦因数
在A正前方距离为s处，有一质量
的小球B，小球B通过长
的细绳与固定点O相连，小物块A与小球B等高，且B始终不与传送带接触
后传送带突然停转，瞬间速度变为零
若A、B发生碰撞后两者将粘在一起绕O点在竖直平面内做圆周运动，并能通过O点正上方的最高点
、B可视为质点，
，求：
、B碰撞后瞬间，细绳拉力的最小值．
刚开始时，A与B的距离s应满足的关系．
【答案】
24N．
．
【解析】
(1)设A、B粘在一起后恰好可以通过最高点，在最高点，对整体由牛顿第二定律可得：
，
对整体由机械能守恒定律可得：
，
在最低点，对整体由牛顿第二定律可得：
联立并代入数据解得：
N，
，
则A、B碰撞后瞬间，细绳拉力的最小值为24N．
(2)对A、B碰撞过程中，系统动量守恒，以A的初速度方向为正方向，由动量守恒可得：
，
代入数据解得：
，
对A，由牛顿第二定律可得：
，
，
若A是在加速阶段与B碰撞，则有：
，
若A是在减速阶段与B碰撞，则A加速运动的时间：
，
A匀速运动的时间：
，
A减速运动的最长时间
s，
各自对应的位移是：
，
，
，
总位移
，
综上可得：A与B的距离s要满足的关系为
．
练习册系列答案
相关题目
