��Ŀ����
����Ŀ����ͼ��ʾ��һ������Ϊ0.4kg��С���Ӹ�h=0.05m�����涥���ɾ�ֹ�ͷţ�����ˮƽ̨�ϣ�����һ�ξ���ӱ�ԵO��ˮƽ�ɳ�������ƽ̨���²൲���ϵ�P�㣮����OΪԭ������ֱ���ڽ�����ͼ��ʾ��ƽ��ֱ������ϵ���������״���㷽��y=x2��6����λ��m��������һ��Ħ���Ϳ���������g=10m/s2 �� ������˵����ȷ���ǣ� �� 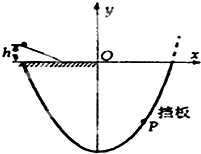
A.С����ˮƽ̨��O��ɳ����ٶȴ�СΪ1m/s
B.С����O���˶���P���ʱ��Ϊl s
C.С���յ�P��ʱ�ٶȷ�����ˮƽ����нǵ�����ֵ����10
D.С���յ�P��ʱ�ٶȵĴ�СΪ10 m/s
���𰸡�ABC
���������⣺A����С��飬���ͷ�������O��Ĺ����У��ɶ��ܶ����ã� mgh= ![]() ��
��
�������ݽ�ã�v= ![]() m/s=1m/s����A��ȷ��
m/s=1m/s����A��ȷ��
B��С����O��ˮƽ�׳���ƽ���˶���
��ֱ����y=�� ![]() ��
��
ˮƽ����x=v0t��
��ã�y=��5x2��
����y=x2��6��
������ã�x=1m��y=��5m��
����h= ![]() ��
��
��ã�t= 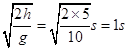 ����B��ȷ��
����B��ȷ��
C����ֱ������ٶȴ�СΪ��vy=gt=10��1=10m/s��
��յ�P��ʱ�ٶȷ�����ˮƽ����н�Ϊ�ȣ����У�tan��= ![]() ����C��ȷ��
����C��ȷ��
D�������ٶȵĺϳɷ������иյ�P��ʱ�ٶȵĴ�СΪ��v= ![]() m/s
m/s ![]() m/s����D����
m/s����D����
��ѡ��ABC��
��С����ɶ��ܶ���������������ٶȣ������ƽ���˶���Ӧ��ƽ���˶����ɿ������P����ٶȴ�С�뷽��ʱ�䣬�Ӷ�������⣮