题目内容
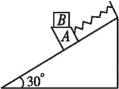
【题目】如图所示，半径R=1.6m的
光滑圆弧轨道位于竖直平面内，与长L=3m的绝缘水平传送带平滑连接，传送带以v=3m/s的速度顺时针转动，传送带右侧空间存在互相垂直的匀强电场和匀强磁场，电场强度E=20N/C，方向竖直向上；磁感应强度B=3.0T，方向垂直纸面向外。两个质量均为m=1.0×10-3Kg的物块a和b，物块a不带电，b带q=1.0×10-3C的正电并静止于圆弧轨道最低点，将a物块从圆弧轨道顶端由静止释放，运动到最低点与b发生正碰，碰撞时间极短，碰后粘合在一起，离开传送带后一起飞入复合场中，最后以与水平成60o角落在地面上的P点（如图），已知两物块与传送带之间的动摩擦因数均为μ=0.1，取g=10m/s2，a、b均可看做质点。求：
（1）物块a运动到圆弧轨道最低点时（碰撞前）对轨道的压力；
（2）传送带距离水平地面的高度；
（3）两物块碰撞后到落地前瞬间的运动过程中，a、b系统机械能的变化量。
【答案】（1）2×10-2N方向竖直向下（2）3m（3）-5.5×10-2J
【解析】
(1)a物块从释放运动到圆弧轨道最低点C时，机械能守恒: 
解得：
在C点，由牛顿第二定律：
解得：
由牛顿第三定律，a物块对圆弧轨道压力
，方向竖直向下
(2)ab碰撞动量守恒：
解得：
ab在传送带上假设能与传送带达到共速时经过的位移为s，由牛顿第二定律：
解得：a=1m/s2
根据速度位移公式：
解得：
<L
所以ab离开传送带时与其共速为v=3m/s，进入复合场后，
，所以做匀速圆周运动，由
，可得：
由几何知识解得传送带与水平地面的高度：
(3)ab系统在传送带上运动过程中，摩擦力对其做功：
ab系统在复合场运动过程中，电场力对其做功：
所以，二者碰后一直到落地，系统机械能的变化量：
△E=Wf+W电=5.5×10-2J
