题目内容
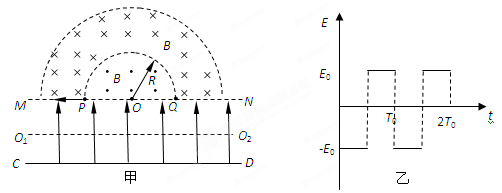
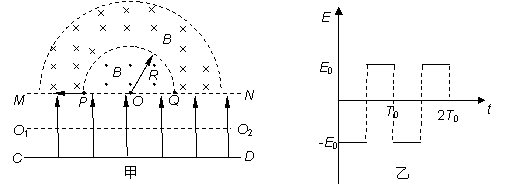
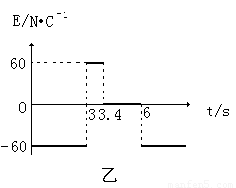
如图甲所示,CD和MN之间存在着变化的电场,电场变化规律如图乙所示,(图中电场方向为正方向),MN为一带电粒子可以自由通过的理想边界,直线MN下方无磁场,上方两个同心半圆内存在着有理想边界的匀强磁场,其分界线是半径为R和2R的半圆,半径为R的圆两侧的磁场方向相反且垂直于纸面,磁感应强度大小都为B。现有一质量为m、电荷量为q的带负电微粒在t=0时刻从O2点沿MN、CD间的中心线O2O1水平向左射入电场,到达P点时以水平向左的速度进入磁场,最终打在Q点。不计微粒的重力。求:
(1)微粒在磁场中运动的周期T;
(2)微粒在电场中的运动时间t1与电场的变化周期T0之间的关系;
(3)MN、CD之间的距离d;
(4)微粒在磁场中运动的半径r的可能值的表达式及r的最大值。
(1)洛仑兹力提供向心力 ![]() ………(2分)
………(2分)
![]() ………(1分)
………(1分)
![]() ………(1分)
………(1分)
(2)由题意分析可知:微粒在竖直方向的运动加速和减速的时间是相等的
则t1=![]() (k=1,2,3…)………(3分,漏k的范围扣1分)
(k=1,2,3…)………(3分,漏k的范围扣1分)
(3)微粒运动的加速度大小![]() ………(1分)
………(1分)
![]() 时间内带电粒子的位移大小
时间内带电粒子的位移大小![]() ………(2分)
………(2分)
![]() (k=1,2,3…) ………(1分)
(k=1,2,3…) ………(1分)
![]() (k=1,2,3…)………(1分)
(k=1,2,3…)………(1分)
(4)粒子的运动轨迹将磁场边界分成![]() 等分(
等分(![]() =2,3,4…)
=2,3,4…)
由几何知识可得:![]() ………(1分)
………(1分)
![]()
![]() ………(1分)
………(1分)
由于有边界限制,须有:
x+r<2R………(1分)
由几何关系可知
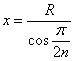
则有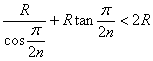 ………………………(1分)
………………………(1分)
得到 ![]()
当![]() 时不成立,如图,故
时不成立,如图,故![]() =3,4,5…
=3,4,5…
经分析可知,n越大,r就越小。………………………………(1分)
当![]() =3时,半径r 有最大值,最大值
=3时,半径r 有最大值,最大值![]() ………(1分)
………(1分)
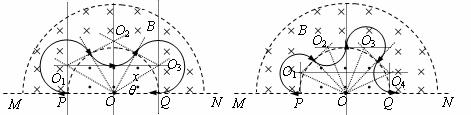

练习册系列答案
相关题目

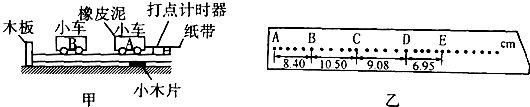
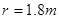 的光滑绝缘圆弧轨道,其所对应的圆心角
的光滑绝缘圆弧轨道,其所对应的圆心角 ,轨道末端水平。木板B长
,轨道末端水平。木板B长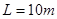 、质量
、质量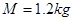 ,静止放置在粗糙水平地面MN上,左端位于M点,上表面与CD轨道末端相切。PQ左侧为匀强磁场区域,磁感应强度
,静止放置在粗糙水平地面MN上,左端位于M点,上表面与CD轨道末端相切。PQ左侧为匀强磁场区域,磁感应强度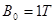 ,方向垂直纸面向外。PQ右侧为匀强电场区域,电场强度随时间变化的关系如图乙所示,规定电场方向竖直向下为正方向。一质量
,方向垂直纸面向外。PQ右侧为匀强电场区域,电场强度随时间变化的关系如图乙所示,规定电场方向竖直向下为正方向。一质量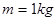 、带电量
、带电量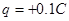 的滑块A在某一时刻由C点静止释放。已知滑块A与木板B之间的动摩擦因素
的滑块A在某一时刻由C点静止释放。已知滑块A与木板B之间的动摩擦因素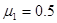 ,木板B与水平地面之间的动摩擦因素
,木板B与水平地面之间的动摩擦因素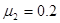 ,可将滑块视为质点,
,可将滑块视为质点,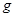 取
取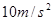 。求:
。求: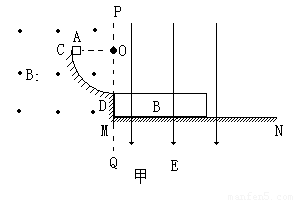
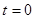 时进入电场区域,滑块A最终静止时离D点的距离。
时进入电场区域,滑块A最终静止时离D点的距离。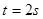 时进入电场区域,滑块A最终静止时离D点的距离。
时进入电场区域,滑块A最终静止时离D点的距离。