题目内容
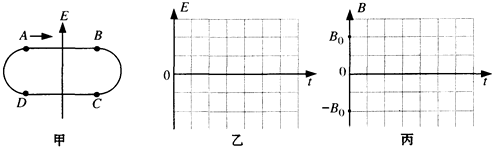
如图甲所示,CD为半径r=1.8m的光滑绝缘圆弧轨道,其所对应的圆心角θ=90°,轨道末端水平.木板B长L=10m、质量M=1.2kg,静止放置在粗糙水平地面MN上,左端位于M点,上表面与CD轨道末端相切.PQ左侧为匀强磁场区域,磁感应强度B0=1T,方向垂直纸面向外.PQ右侧为匀强电场区域,电场强度随时间变化的关系如图乙所示,规定电场方向竖直向下为正方向.一质量m=1kg、带电量q=+0.1C的滑块A在某一时刻由C点静止释放.已知滑块A与木板B之间的动摩擦因素μ1=0.5,木板B与水平地面之间的动摩擦因素μ2=0.2,可将滑块视为质点,g取10m/s2.求:
(1)滑块A滑至圆弧轨道最低点时的速度大小和此时滑块A对轨道的压力.
(2)若滑块A在t=0时进入电场区域,滑块A最终静止时离D点的距离.
(3)若滑块A在t=2s时进入电场区域,滑块A最终静止时离D点的距离.

(1)滑块A滑至圆弧轨道最低点时的速度大小和此时滑块A对轨道的压力.
(2)若滑块A在t=0时进入电场区域,滑块A最终静止时离D点的距离.
(3)若滑块A在t=2s时进入电场区域,滑块A最终静止时离D点的距离.

分析:(1)小物块从C处运动到D点的过程中,只有重力做功,机械能守恒.根据机械能守恒,得出小物块滑到D点时的速度大小v.
(2)先求滑块与木板的摩擦力和木板与地面的摩擦力,判断出木板不动,应用运动学知识求解.
(3)滑块在周期性变化的电场中做匀变速直线运动,根据运动学知识求每个运动过程的加速度,速度,位移,最后加和.
(2)先求滑块与木板的摩擦力和木板与地面的摩擦力,判断出木板不动,应用运动学知识求解.
(3)滑块在周期性变化的电场中做匀变速直线运动,根据运动学知识求每个运动过程的加速度,速度,位移,最后加和.
解答:解:(1)从C到D,物体机械能守恒:mgr=
mV2
解得:V=
=6m/s
由向心力公式知:N-mg-qVB=
解得:N=30.6N,方向竖直向上,
由牛顿第三定律知对轨道的压力为30.6N,方向竖直向下
(2)A与B间的摩擦力:f1=μ1(mg-qE)=2N
B与水平面间的摩擦力:f2=μ2(mg+Mg-qE)=3.2N
f1<f2,所以木板不动:a=
=2m/S2
滑块静止用时:t=
=3s,电场方向恰好未改变,
滑行距离:S=
=9m<L,未从木板滑落
所以A静止时离D的距离为9m
(3)从2S到3S过程中,滑块加速度:a=2m/s2,
3S时滑块速度:V1=V-at1=4m/s
此过程中滑块的位移:S1=
(V+V1)t1=5m
此后电场反向:f1′=μ1(mg+qE)=8N
f2′=μ2(Mg+mg+qE)=5.6N
所以木板加速运动,此时AB的加速度分别为:a1=
=8m/S2
a2=
=2m/S2
速度相等用时t2:V1-a1t2=a2t2
解得:t2=0.4S
共同速度:v2=a2t2=0.8m/s
此过程中位移:S2=
(V1+V2)t2=0.96m
此后电场强度为零,二者共同减速运动:a′=
=2m/S2
到静止用时:t3=
=0.4S
此过程位移:S3=
=0.16m
所以整个过程的位移:S=S1+S2+S3=6.12m
答:(1)滑块A滑至圆弧轨道最低点时的速度大小6m/s
此时滑块A对轨道的压力30.6N,方向竖直向上.
(2)若滑块A在t=0时进入电场区域,滑块A最终静止时离D点的距离9m.
(3)若滑块A在t=2s时进入电场区域,滑块A最终静止时离D点的距离6.12m.
| 1 |
| 2 |
解得:V=
| 2gr |
由向心力公式知:N-mg-qVB=
| mV2 |
| r |
解得:N=30.6N,方向竖直向上,
由牛顿第三定律知对轨道的压力为30.6N,方向竖直向下
(2)A与B间的摩擦力:f1=μ1(mg-qE)=2N
B与水平面间的摩擦力:f2=μ2(mg+Mg-qE)=3.2N
f1<f2,所以木板不动:a=
| f1 |
| m |
滑块静止用时:t=
| V |
| a |
滑行距离:S=
| V2 |
| 2a |
所以A静止时离D的距离为9m
(3)从2S到3S过程中,滑块加速度:a=2m/s2,
3S时滑块速度:V1=V-at1=4m/s
此过程中滑块的位移:S1=
| 1 |
| 2 |
此后电场反向:f1′=μ1(mg+qE)=8N
f2′=μ2(Mg+mg+qE)=5.6N
所以木板加速运动,此时AB的加速度分别为:a1=
| f1′ |
| m |
a2=
| f1′-f2′ |
| M |
速度相等用时t2:V1-a1t2=a2t2
解得:t2=0.4S
共同速度:v2=a2t2=0.8m/s
此过程中位移:S2=
| 1 |
| 2 |
此后电场强度为零,二者共同减速运动:a′=
| μ2(Mg+mg) |
| M+m |
到静止用时:t3=
| V2 |
| a′ |
此过程位移:S3=
| ||
| 2a′ |
所以整个过程的位移:S=S1+S2+S3=6.12m
答:(1)滑块A滑至圆弧轨道最低点时的速度大小6m/s
此时滑块A对轨道的压力30.6N,方向竖直向上.
(2)若滑块A在t=0时进入电场区域,滑块A最终静止时离D点的距离9m.
(3)若滑块A在t=2s时进入电场区域,滑块A最终静止时离D点的距离6.12m.
点评:该题是一道综合题,综合运用了机械能守恒定律、牛顿第二定律以及牛顿第三定律,解决本题的关键熟练这些定理、定律的运用.

练习册系列答案
相关题目
 某种发电机的内部结构平面图如图甲,永磁体的内侧为半圆柱面形,它与圆柱形铁芯之间的窄缝间形成如图所示B=0.5T的磁场.在磁场中有一个如图乙所示的U形导线框abcd.已知线框ab和cd边长均为0.2m,bc边长为0.4m,线框以ω=200πrad/s角速度顺时针匀速转动.
某种发电机的内部结构平面图如图甲,永磁体的内侧为半圆柱面形,它与圆柱形铁芯之间的窄缝间形成如图所示B=0.5T的磁场.在磁场中有一个如图乙所示的U形导线框abcd.已知线框ab和cd边长均为0.2m,bc边长为0.4m,线框以ω=200πrad/s角速度顺时针匀速转动. 求t=2.5×10-3s这一时刻线框中感应电动势的大小,并在给定的坐标平面内画出ad两点电势差Uad随时间变化的关系图线.(感应电动势的结果保留两位有效数字,Uad正值表示Ua>Ud)
求t=2.5×10-3s这一时刻线框中感应电动势的大小,并在给定的坐标平面内画出ad两点电势差Uad随时间变化的关系图线.(感应电动势的结果保留两位有效数字,Uad正值表示Ua>Ud)
