题目内容
12.最近,科学家在望远镜中看到太阳系外某一恒星系中的一行星,并测得它围绕该恒星运动一周所用的时间为1 200年,它与该恒星的距离为地球到太阳距离的100倍.假定该行星绕恒星运动的轨道和地球绕太阳运动的轨道都是圆周,仅利用以上两个数据可以求出的量有( )| A. | 行星的向心力与地球的向心力之比 | |
| B. | 恒星的密度与太阳的密度之比 | |
| C. | 恒星的质量与太阳的质量之比 | |
| D. | 行星的向心加速度与地球公转向心加速度之比 |
分析 根据行星的万有引力等于向心力,结合行星的轨道半径和公转周期列式求出恒星质量的表达式进行讨论即可.
解答 解:行星绕恒星做匀速圆周运动,设恒星质量为M,行星质量为m,轨道半径为r,根据万有引力提供向心力得:
$\frac{GMm}{{r}^{2}}=\frac{m4{π}^{2}r}{{T}^{2}}$
得:$M=\frac{4{π}^{2}{r}^{3}}{G{T}^{2}}$…①
故太阳的质量为:$M′=\frac{4{π}^{2}r{′}^{2}}{GT{′}^{2}}$…②
A、由于不知道行星和地球质量的关系,所以无法求得行星的向心力与地球的向心力之比,故A错误;
B、恒星的密度为:$ρ=\frac{M}{V}=\frac{\frac{4π{{\;}^{2}r}^{3}}{G{T}^{2}}}{\frac{4}{3}π{R}^{3}}=\frac{3π{r}^{3}}{G{T}^{2}{R}^{3}}$,由于不知道恒星和太阳的半径,所以无法求得恒星的密度与太阳的密度之比,故B错误;
C、由于地球的公转周期为1年,根据①②式可以求得恒星质量与太阳质量之比,故C正确;
D、根据$a=\frac{4{π}^{2}r}{{T}^{2}}$且已知行星和地球的轨道半径和周期关系,故可求行星的向心加速度与地球公转向心加速度之比,故D正确;
故选:CD.
点评 本题关键是根据行星做匀速圆周运动,万有引力提供向心力,列方程求出太阳和恒星的质量和环绕速度,然后分析即可.

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案
相关题目
3.如图,三卫星分别处在轨道1、轨道2、轨道3,其中轨道2为同步卫星轨道,下列说法正确的是( )
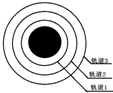

| A. | 轨道3的线速度最大,轨道1的线速度最小 | |
| B. | 轨道3的向心力最小,轨道1的向心力最大 | |
| C. | 轨道2的周期为24小时 | |
| D. | 轨道3的周期最大,轨道1的周期最小 |
7.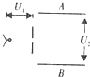 如图,电子(不计重力,电荷量为e,质量为m)由静止经加速电场加速,然后从相互平行的AB两板的正中间射入,已知加速电场两极间电压为U1,AB两板之间电压为U2,则下列说法中正确的是( )
如图,电子(不计重力,电荷量为e,质量为m)由静止经加速电场加速,然后从相互平行的AB两板的正中间射入,已知加速电场两极间电压为U1,AB两板之间电压为U2,则下列说法中正确的是( )
 如图,电子(不计重力,电荷量为e,质量为m)由静止经加速电场加速,然后从相互平行的AB两板的正中间射入,已知加速电场两极间电压为U1,AB两板之间电压为U2,则下列说法中正确的是( )
如图,电子(不计重力,电荷量为e,质量为m)由静止经加速电场加速,然后从相互平行的AB两板的正中间射入,已知加速电场两极间电压为U1,AB两板之间电压为U2,则下列说法中正确的是( )| A. | 电子穿过AB板时,其动能一定等于e(U1+$\frac{{U}_{2}}{2}$) | |
| B. | 为使电子能飞出AB板,则要求U1>U2 | |
| C. | 若把电子换成另一种带负电的粒子(忽略重力),它将沿着电子的运动轨迹运动 | |
| D. | 在AB板间,沿电子运动轨迹的电势越来越低 |
17.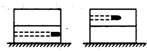 矩形滑块由不同材料的上、下两层粘合在一起组成,将其放在光滑的水平面上,质量为m的子弹以速度v水平射向滑块.若射击下层,子弹刚好不射出;若射击上层,则子弹刚好能射穿一半厚度,如图所示.则上述两种情况相比较( )
矩形滑块由不同材料的上、下两层粘合在一起组成,将其放在光滑的水平面上,质量为m的子弹以速度v水平射向滑块.若射击下层,子弹刚好不射出;若射击上层,则子弹刚好能射穿一半厚度,如图所示.则上述两种情况相比较( )
 矩形滑块由不同材料的上、下两层粘合在一起组成,将其放在光滑的水平面上,质量为m的子弹以速度v水平射向滑块.若射击下层,子弹刚好不射出;若射击上层,则子弹刚好能射穿一半厚度,如图所示.则上述两种情况相比较( )
矩形滑块由不同材料的上、下两层粘合在一起组成,将其放在光滑的水平面上,质量为m的子弹以速度v水平射向滑块.若射击下层,子弹刚好不射出;若射击上层,则子弹刚好能射穿一半厚度,如图所示.则上述两种情况相比较( )| A. | 子弹的末速度大小相等 | B. | 系统产生的热量一样多 | ||
| C. | 子弹对滑块做的功相同 | D. | 子弹和滑块间的水平作用力一样大 |
4.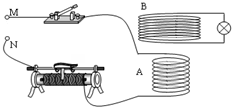 如图所示,线圈A、电键和滑动变阻器相连后接入M、N间的电源,B为一接有小灯珠的闭合线圈,下列关于小灯珠发光说法正确的是( )
如图所示,线圈A、电键和滑动变阻器相连后接入M、N间的电源,B为一接有小灯珠的闭合线圈,下列关于小灯珠发光说法正确的是( )
 如图所示,线圈A、电键和滑动变阻器相连后接入M、N间的电源,B为一接有小灯珠的闭合线圈,下列关于小灯珠发光说法正确的是( )
如图所示,线圈A、电键和滑动变阻器相连后接入M、N间的电源,B为一接有小灯珠的闭合线圈,下列关于小灯珠发光说法正确的是( )| A. | 当电源是交流电源时,闭合电键后小灯珠可能发光 | |
| B. | 若闭合电键后小灯珠发光,则再将B线圈靠近A,则小灯珠更亮 | |
| C. | 当电源是交流电源时,闭合电键瞬间,小灯珠才能发光 | |
| D. | 当电源是直流电源时,无论如何操作小灯珠一定不发光 |
1.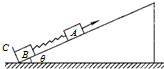 在倾角为θ的光滑固定斜面上有两个用轻弹簧连接的物块A和B,它们的质量分别为m和2m,弹簧的劲度系数为k,C为一固定挡板,系统处于静止状态.现用一沿斜面方向的恒力拉物块A使之沿斜面向上运动,当B刚离开C时,A的速度为v,加速度为a,且方向沿斜面向上.设弹簧始终处于弹性限度内,重力加速度为g,则( )
在倾角为θ的光滑固定斜面上有两个用轻弹簧连接的物块A和B,它们的质量分别为m和2m,弹簧的劲度系数为k,C为一固定挡板,系统处于静止状态.现用一沿斜面方向的恒力拉物块A使之沿斜面向上运动,当B刚离开C时,A的速度为v,加速度为a,且方向沿斜面向上.设弹簧始终处于弹性限度内,重力加速度为g,则( )
 在倾角为θ的光滑固定斜面上有两个用轻弹簧连接的物块A和B,它们的质量分别为m和2m,弹簧的劲度系数为k,C为一固定挡板,系统处于静止状态.现用一沿斜面方向的恒力拉物块A使之沿斜面向上运动,当B刚离开C时,A的速度为v,加速度为a,且方向沿斜面向上.设弹簧始终处于弹性限度内,重力加速度为g,则( )
在倾角为θ的光滑固定斜面上有两个用轻弹簧连接的物块A和B,它们的质量分别为m和2m,弹簧的劲度系数为k,C为一固定挡板,系统处于静止状态.现用一沿斜面方向的恒力拉物块A使之沿斜面向上运动,当B刚离开C时,A的速度为v,加速度为a,且方向沿斜面向上.设弹簧始终处于弹性限度内,重力加速度为g,则( )| A. | 当B刚离开C时,A发生的位移大小为$\frac{3mgsinθ}{k}$ | |
| B. | 从静止到B刚离开C的过程中,物块A克服重力做功为$\frac{3{m}^{2}{g}^{2}sinθ}{k}$ | |
| C. | B刚离开C时,恒力对A做功的功率为(2mgsinθ+ma)v | |
| D. | 当A的速度达到最大时,B的加速度大小为$\frac{a}{2}$ |
2. 至今为止,我国北斗导航系统(BDS)已经全部完成了第二阶段的卫星发射任务,共有16颗卫星在工作,其中包括5颗地球静止轨道卫星,有关这16颗卫星,下列说法正确的是( )
至今为止,我国北斗导航系统(BDS)已经全部完成了第二阶段的卫星发射任务,共有16颗卫星在工作,其中包括5颗地球静止轨道卫星,有关这16颗卫星,下列说法正确的是( )
 至今为止,我国北斗导航系统(BDS)已经全部完成了第二阶段的卫星发射任务,共有16颗卫星在工作,其中包括5颗地球静止轨道卫星,有关这16颗卫星,下列说法正确的是( )
至今为止,我国北斗导航系统(BDS)已经全部完成了第二阶段的卫星发射任务,共有16颗卫星在工作,其中包括5颗地球静止轨道卫星,有关这16颗卫星,下列说法正确的是( )| A. | 卫星的质量可以都不相同 | |
| B. | 卫星的绕行方向可以都不相同 | |
| C. | 卫星的轨道半径可以都不相同 | |
| D. | 5颗地球静止轨道卫星轨道平面都相同 |
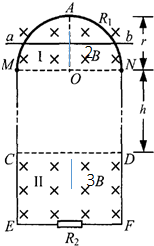 如图所示,竖直平面内有一半径为r、电阻为R1、粗细均匀的光滑半圆形金属环,在M、N处与相距为2r、电阻不计的平行光滑金属轨道ME、NF相接,EF之间接有电阻R2,已知R1=12R,R2=4R.在MN上方及CD下方有水平方向的匀强磁场I和II,磁场I的磁感应强度大小为2B;磁场II的磁感应强度为3B.现有质量为m、电阻不计的导体棒ab,从半圆环的最高点A处由静止开始下落,在下落过程中导体棒始终保持水平,与半圆形金属环及轨道接触良好,平行轨道足够长.已知导体棒ab下落$\frac{r}{2}$时的速度大小为v1,下落到MN处的速度大小为v2.
如图所示,竖直平面内有一半径为r、电阻为R1、粗细均匀的光滑半圆形金属环,在M、N处与相距为2r、电阻不计的平行光滑金属轨道ME、NF相接,EF之间接有电阻R2,已知R1=12R,R2=4R.在MN上方及CD下方有水平方向的匀强磁场I和II,磁场I的磁感应强度大小为2B;磁场II的磁感应强度为3B.现有质量为m、电阻不计的导体棒ab,从半圆环的最高点A处由静止开始下落,在下落过程中导体棒始终保持水平,与半圆形金属环及轨道接触良好,平行轨道足够长.已知导体棒ab下落$\frac{r}{2}$时的速度大小为v1,下落到MN处的速度大小为v2. 2014年12月26日,我国东部14省市ETC联网正式启动运行,ETC是电子不停车收费系统的简称,汽车分别通过ETC通道和人工收费通道的流程如图所示,假设道路上有并行的甲、乙两汽车都以v1=20m/s朝收费站正常沿直线行驶,现加成过ETC通道,需要在某位置开始做匀减速运动,到达虚线EF处处速度正好减为v2=4m/s,在虚线EF与收费站中心线之间以4m/s的速度匀速行驶,通过收费站中心线后才加速行驶离开,已知甲匀减速过程的加速度大小为a1=1m/s2,虚线EF处与收费站中心线距离d=10m,乙车过人工收费通道,需要在中心线某位置开始做匀减速运动,至中心线处恰好速度为零,进过缴费成功后再启动汽车行驶离开,已知乙车匀减速过程的加速度大小为a2=2m/s2,求:
2014年12月26日,我国东部14省市ETC联网正式启动运行,ETC是电子不停车收费系统的简称,汽车分别通过ETC通道和人工收费通道的流程如图所示,假设道路上有并行的甲、乙两汽车都以v1=20m/s朝收费站正常沿直线行驶,现加成过ETC通道,需要在某位置开始做匀减速运动,到达虚线EF处处速度正好减为v2=4m/s,在虚线EF与收费站中心线之间以4m/s的速度匀速行驶,通过收费站中心线后才加速行驶离开,已知甲匀减速过程的加速度大小为a1=1m/s2,虚线EF处与收费站中心线距离d=10m,乙车过人工收费通道,需要在中心线某位置开始做匀减速运动,至中心线处恰好速度为零,进过缴费成功后再启动汽车行驶离开,已知乙车匀减速过程的加速度大小为a2=2m/s2,求: