题目内容
3.一根轻质弹簧一端固定,用大小为F1的力压弹簧的另一端,平衡时长度为L1;改用大小为F2的力拉弹簧,平衡时长度为L2.弹簧的拉伸或压缩均在弹性限度内,该弹簧的劲度系数为$\frac{{{F_1}+{F_2}}}{{{L_2}-{L_1}}}$.分析 根据弹簧受F1、F2两个力的作用时的弹簧的长度,分别由胡克定律列出方程联立求解即可.
解答 解:由胡克定律得 F=kx,式中x为形变量,
设弹簧原长为l0,则有
F1=k(l0-l1),
F2=k(l2-l0),
联立方程组可以解得 k=$\frac{{F}_{1}+{F}_{2}}{{l}_{2}-{l}_{1}}$.
故答案为:$\frac{{F}_{1}+{F}_{2}}{{l}_{2}-{l}_{1}}$
点评 本题考查胡克定律的计算,在利用胡克定律 F=kx计算时,一定要注意式中x为弹簧的形变量,不是弹簧的长度,这是同学常出差的一个地方.

练习册系列答案
相关题目
20.一只矩形线圈在匀强磁场中转动,产生的交流电动势e=10$\sqrt{2}$sin4πtV,下列叙述正确的是( )
| A. | 交流电的峰值10$\sqrt{2}$V | B. | 交流电的有效值是10V | ||
| C. | 交变电的周期是0.5s | D. | 当t=$\frac{1}{2}$s时,e有最大值 |
1.2011年7月11日23时41分,我国在西昌卫星发射中心用长征三号丙运载火箭,成功将“天链一号02星”送入太空,并成功进入地球同步转移轨道,“天链一号02星”是我国第二颗地球同步轨道数据中继卫星,它将与2008年发射的“天链一号01星”组网运行,为我国神州飞船以及未来空间实验室、空间站建设提供数据中继和测控服务,并将应用于我国将于2011年下半年实施的首次空间交会对接任务,下列说法不正确的是( )
| A. | “天链一号01星”、“天链一号02星”的发射速度大于11.2km/s,运行速度小于7.9km/s | |
| B. | “天链一号01星”、“天链一号02星”在预定轨道正常运动时,都一定位于赤道的正上方 | |
| C. | “天链一号01星”、“天链一号02星”向心加速度与静止在赤道上物体的向心加速度大小不相等 | |
| D. | “天链一号01星”、“天链一号02星”与地球间的万有引力大小可能不相同 |
8.要使放在水平地面上重600N的木箱开始移动,最小要用200N的水平推力,已知木箱与地面间的动摩擦因数为0.3,那么( )
| A. | 若用160N的水平力推木箱时,木箱受到的摩擦力为160N | |
| B. | 若用180N的水平力推木箱时,木箱开始滑动 | |
| C. | 若用250N的水平力推木箱时,木箱受到的摩擦力为180N | |
| D. | 若用200N的水平力推木箱时,木箱沿着水平力方向滑动,做匀速直线运动 |
15.湖中O处有一观察站,一小船从O处出发向东行驶4km,又向北行驶3km,则下列说法中正确的是( )
| A. | 相对于O处的观察员,小船向东北方向运动了7 km | |
| B. | 相对于小船,O处的观察员始终处于静止状态 | |
| C. | 相对于O处的观察员,小船最终位于东偏北37°方向5 km处 | |
| D. | 相对于湖岸上的另一观察员,小船不可能是静止的 |
12.利用如图1所示的实验装置探究“加速度a与力F及物体质量M的定量关系”.其中,A为小车,B为打点计时器,C为装有砂的砂桶(总质量为m),D为一端带有定滑轮的长木板(实验时已经平衡了摩擦力).
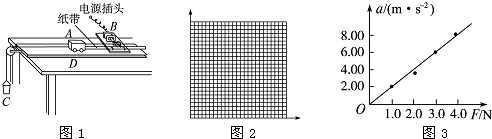
(1)若保持砂和砂桶的质量不变,改变小车的质量M,分别得到小车加速度a与质量M及对应的$\frac{1}{M}$数据如表所示:
①根据表数据,为了反映F不变时a与M的关系,请在图2所示的方格坐标纸中选择恰当的物理量建立坐标系,并作出图象.
②根据图线得出F不变时a与M的关系是a与M成反比.
(2)小车质量一定,探究加速度a与F的关系时,某同学根据测量记录的数据,作出图象如图3所示.
①根据图象得到的结论是在质量一定的情况下,物体的加速度与物体所受的合外力成正比.
②图象斜率的物理意义是物体质量的倒数$\frac{1}{m}$.
③在实验中,我们认为细线的拉力F等于砂桶的重力,实际上细线的拉力F小于砂桶的重力mg(填“大于”“小于”或“等于”).

(1)若保持砂和砂桶的质量不变,改变小车的质量M,分别得到小车加速度a与质量M及对应的$\frac{1}{M}$数据如表所示:
| 序号 | 1 | 2 | 3 | 4 | 5 |
| 小车的加速度a/(m•s-2) | 1.98 | 1.48 | 1.00 | 0.67 | 0.50 |
| 小车质量M/kg | 0.25 | 0.33 | 0.50 | 0.75 | 1.00 |
| 质量倒数$\frac{1}{M}$/kg-1 | 4.00 | 3.00 | 2.00 | 1.33 | 1.00 |
②根据图线得出F不变时a与M的关系是a与M成反比.
(2)小车质量一定,探究加速度a与F的关系时,某同学根据测量记录的数据,作出图象如图3所示.
①根据图象得到的结论是在质量一定的情况下,物体的加速度与物体所受的合外力成正比.
②图象斜率的物理意义是物体质量的倒数$\frac{1}{m}$.
③在实验中,我们认为细线的拉力F等于砂桶的重力,实际上细线的拉力F小于砂桶的重力mg(填“大于”“小于”或“等于”).
 质量m=5×10-6kg的带电小球以v0=2m/s的速度从水平放置的平行金属板A、B中央水平飞入板间,如图所示,已知板长L=10cm,板间距离d=2cm,当UAB=1000V时,带电粒子恰好沿直线穿过板间,则:
质量m=5×10-6kg的带电小球以v0=2m/s的速度从水平放置的平行金属板A、B中央水平飞入板间,如图所示,已知板长L=10cm,板间距离d=2cm,当UAB=1000V时,带电粒子恰好沿直线穿过板间,则: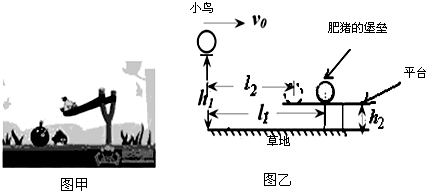
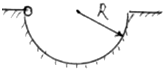 如图所示,质量为m的物体从半径为R的半圆形轨道的边缘由静止开始下滑,滑至最低点时,对轨道压力为2.8mg,则物体从开始到最低点的运动过程中克服阻力做功为0.1mgR.
如图所示,质量为m的物体从半径为R的半圆形轨道的边缘由静止开始下滑,滑至最低点时,对轨道压力为2.8mg,则物体从开始到最低点的运动过程中克服阻力做功为0.1mgR.