��Ŀ����
����Ŀ����ͼ��ʾ����ƽ�е�����L��1.0 m����б����⻬���㹻������ˮƽ��ļн�����30����ˮƽ����ֲ�������б���Բ����������б������д�ֱб�����ϵĴų����Ÿ�Ӧǿ��B��2.5 T��ˮƽ�����û�дų���������ab����m��0.5 kg������r��2.0 �����˶����뵼�������ýӴ������Ҵ�ֱ�ڵ���������R��8.0 ����������費��������������б������ظ߶�h��3.0 m���ɾ�ֹ�ͷ�����������ˮƽ����ϻ��еľ���x��1.25 m�����ҷ��ֽ������Ӹ��ߴ���ֹ�ͷ�����������ˮƽ����ϻ��еľ��벻����(ȡg��10 m/s2)����
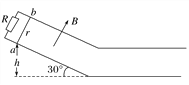
(1)�Ӹ߶�h��3.0 m���ɾ�ֹ�ͷź�������������б���ʱ���ٶȴ�С��
(2)��������ˮƽ�����Ķ�Ħ����������
(3)��������ij�߶�H����ֹ�ͷź����»����˵Ĺ���������R�ĵ���q��2.0 C����ù����е���R�ϲ�����������
���𰸡�(1)4.0 m/s��(2)0.64��(3)12.8 J
��������(1)������֪������������ظ�h��3.0 m�����κεط��ɾ�ֹ�ͷź��ڵ���ˮƽ��֮ǰ���Ѿ���ʼ�����˶���������ٶ�Ϊv�����Ӧ�綯��E��BLv
��Ӧ����I��![]()
������F��BIL
�����˶�ʱ����mgsin ����F
���v��4.0 m/s
(2)��ˮƽ������˶�ʱ�����������ܻ���Ħ����Ff����mg
��������Ħ�������������ȼ����˶�����
Ff��ma
v2��2ax
�������0.64
(3)�»��Ĺ�����
q��![]()
�ã�H��4.0 m>h
�ɶ��ܶ����ɵã�
mgH��W��![]() mv2
mv2
�����������Ĺ����ڵ�·�в����Ľ����ȣ���
Q��W��16 J
����R�ϲ�����������QR��![]() Q
Q
���QR��12.8 J.

 �������Ӧ���⼯ѵϵ�д�
�������Ӧ���⼯ѵϵ�д� �ۺ��Բ�ϵ�д�
�ۺ��Բ�ϵ�д�