题目内容
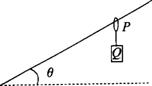
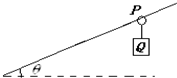 如图所示,套在绳索上的小圆环 P 下面挂一个重为G的物体 Q 并使它们处于静止状态.现释放圆环P,让其沿与水平面成 θ 角的绳索无摩擦的下滑,在圆环 P 下滑过程中绳索处于绷紧状态(可认为是一直线),若圆环和物体下滑时不振动,则下列说法正确的是
如图所示,套在绳索上的小圆环 P 下面挂一个重为G的物体 Q 并使它们处于静止状态.现释放圆环P,让其沿与水平面成 θ 角的绳索无摩擦的下滑,在圆环 P 下滑过程中绳索处于绷紧状态(可认为是一直线),若圆环和物体下滑时不振动,则下列说法正确的是
- A.Q的加速度一定小于 gsinθ
- B.悬线所受拉力为 Gsinθ
- C.悬线所受拉力为Gcosθ
- D.悬线一定与绳索垂直
CD
分析:对圆环与重物的整体分析,根据牛顿第二定律求出加速度的大小,隔离对木块分析,根据合力的大小,得出绳子拉力的大小和方向.
解答:A、对整体分析,根据牛顿第二定律得,a= .则Q的加速度为gsinθ.故A错误.
.则Q的加速度为gsinθ.故A错误.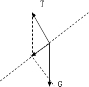
B、隔离对Q分析,知Q的合力为F合=mgsinθ,受重力和拉力两个力的作用,如图所示,根据合力的大小和重力大小关系知,悬线与绳索垂直.拉力T=Gcosθ.故C、D正确,B错误.
故选CD.
点评:解决本题的关键知道圆环与重物具有相同的加速度,通过整体隔离法,运用牛顿第二定律进行分析.
分析:对圆环与重物的整体分析,根据牛顿第二定律求出加速度的大小,隔离对木块分析,根据合力的大小,得出绳子拉力的大小和方向.
解答:A、对整体分析,根据牛顿第二定律得,a=
 .则Q的加速度为gsinθ.故A错误.
.则Q的加速度为gsinθ.故A错误.
B、隔离对Q分析,知Q的合力为F合=mgsinθ,受重力和拉力两个力的作用,如图所示,根据合力的大小和重力大小关系知,悬线与绳索垂直.拉力T=Gcosθ.故C、D正确,B错误.
故选CD.
点评:解决本题的关键知道圆环与重物具有相同的加速度,通过整体隔离法,运用牛顿第二定律进行分析.

练习册系列答案
相关题目
 如图所示,套在绳索上的小圆环 P 下面挂一个重为G的物体 Q 并使它们处于静止状态.现释放圆环P,让其沿与水平面成 θ 角的绳索无摩擦的下滑,在圆环 P 下滑过程中绳索处于绷紧状态(可认为是一直线),若圆环和物体下滑时不振动,则下列说法正确的是( )
如图所示,套在绳索上的小圆环 P 下面挂一个重为G的物体 Q 并使它们处于静止状态.现释放圆环P,让其沿与水平面成 θ 角的绳索无摩擦的下滑,在圆环 P 下滑过程中绳索处于绷紧状态(可认为是一直线),若圆环和物体下滑时不振动,则下列说法正确的是( )