题目内容
（2011?琼海一模）如图，A、B是在地球大气层外圆周轨道上运行的质量不等的两颗卫星，它们的轨道半径满足RA=2R，RB=3R，R为地球半径，下列说法正确的是（ ）分析：A、B两颗卫星绕地球做圆周运动，靠万有引力提供向心力，根据牛顿第二定律求出线速度、角速度、加速度、万有引力与轨道半径的关系，从而得出它们的比值．
解答：解：根据G
=ma=m
=mrω2
得：a=
，v=
，ω=
则：
=
=
=
=
=
=
由于卫星的质量不等，故无法求出A、B受到的万有引力之比．故B、C正确，A、D错误．
故选BC．
| Mm |
| r2 |
| v2 |
| r |
得：a=
| GM |
| r2 |
|
|
则：
| ωA |
| ωB |
|
3
| ||
| 4 |
| vA |
| vB |
|
| ||
|
| aA |
| aB |
| rB2 |
| rA2 |
| 9 |
| 4 |
由于卫星的质量不等，故无法求出A、B受到的万有引力之比．故B、C正确，A、D错误．
故选BC．
点评：解决本题的关键知道卫星绕地球做圆周运动靠万有引力提供向心力，掌握线速度、角速度、周期、加速度与轨道半径的关系．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
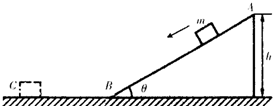（2011?琼海一模）如图所示，抗震救灾运输机在某场地卸放物资时，通过倾角θ=30°的固定的光滑斜轨道面进行．有一件质量为m=2.0kg的小包装盒，由静止开始从斜轨道的顶端A滑至底端B，然后又在水平地面上滑行一段距离停下，若A点距离水平地面的高度h=5.0m，重力加速度g取10m/s2，求：
（2011?琼海一模）如图所示，左右两个容器的侧壁都是绝热的、底部都是导热的、横截面积均为S．左容器足够高，上端敞开，右容器上端由导热材料封闭．两个容器的下端由容积可忽略的细管连通．容器内两个绝热的活塞A、B下方封有氮气，B上方封有氢气．大气的压强为p0，外部气温为T0=273K保持不变，两个活塞因自身重力对下方气体产生的附加压强均为0.1p0．系统平衡时，各气体柱的高度如图所示．现将系统的底部浸入恒温热水槽中，再次平衡时A上升了一定的高度．用外力将A缓慢推回第一次平衡时的位置并固定，第三次达到平衡后，氢气柱高度为0.8h．氮气和氢气均可视为理想气体．求：
（2011?琼海一模）M、N是一对水平放置的平行板电容器，将它与一电动势为E，内阻为r的电源组成如图所示的电路，R是并联在电容器上的滑动变阻器，G是灵敏电流计，在电容器的两极板间有一带电的油滴处于悬浮状态，如图所示，现保持开关S闭合，将滑动变阻器的滑片向上滑动，则（ ）