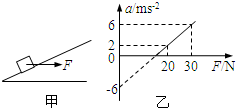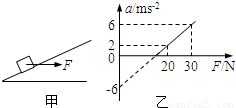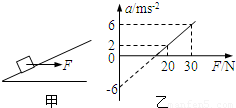Question

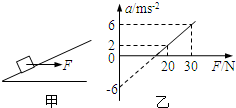如图甲所示，用水平力F拉着一个静止在倾角为θ的光滑斜面上的物体，逐渐增大F，物体做变加速运动，其加速度a随外力F变化的图象如图乙所示，根据图乙中所提供的信息可以计算出（　　）

A．物体的质量2kg

B．斜面的倾角37°

C．加速度为6m/s²时物体的速度

D．物体能静止在斜面上所施加的最小外力为12N

Answer 1

分析：对物体受力分析，根据牛顿第二定律列式求解出加速度表达式，再进行分析处理．

解答：解：对物体受力分析，如图

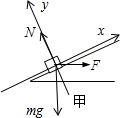
根据牛顿第二定律，有
Fcosθ-mgsinθ=ma
解得
a=

Fcosθ

m

-gsinθ
由a与F图线，得到
-gsinθ=-6

cosθ

m

=

6-2

30-20

解得
θ=37°
m=2kg
故a=0时，F为15N；
故选AB．

点评：本题关键是对滑块受力分析，然后根据牛顿第二定律列方程求解出加速度与推力F的关系式，最后结合a与F关系图象得到待求量．