题目内容
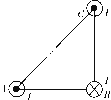
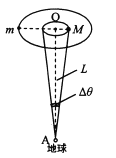
【题目】如图所示，双星系统由质量不相等的两颗恒星组成，质量分别是M、m(M>m)， 他们围绕共同的圆心O做匀速圆周运动。从地球A看过去，双星运动的平面与AO垂直，AO距离恒为L。观测发现质量较大的恒星M做圆周运动的周期为T，运动范围的最大张角为△θ(单位是弧度)。已知引力常量为G，△θ很小，可认为sin△θ= tan△θ= △θ，忽略其他星体对双星系统的作用力。则
A. 恒星m的角速度大小为
B. 恒星m的轨道半径大小为
C. 恒星m的线速度大小为
D. 两颗恒星的质量m和M满足关系式
【答案】BCD
【解析】恒星m与M具有相同的角速度，则角速度为
，选项A错误；恒星M的轨道半径为
；对恒星系统： mω2r=Mω2R，解得恒星m的轨道半径大小为
，选项B正确；恒星m的线速度大小为
，选项C正确；对恒星系统： 
=mω2r=Mω2R，解得GM=ω2r(r+R)2；Gm=ω2R(r+R)2；相加得：
，联立可得：
，选项D正确；故选BCD.
练习册系列答案
相关题目
