题目内容
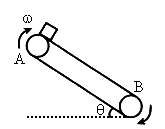
如图所示,AB两轮间距L=3.25m,套有传送带,传送带与水平面成θ=30°角.轮子转动方向如图所示,使传送带始终以2m/s的速率运行,将一物体无初速度地放到A轮处的传送带上,物体与传送带间的动摩擦因数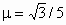 ,求物体从A运动到B所需的时间.
,求物体从A运动到B所需的时间.

答案:1.25s
解析:
解析:
|
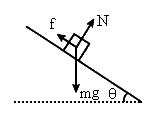
由物体与传送带间的相对运动分析物体所受滑动摩擦力是解答本题的关键,物体刚被放到 A处的传送带上时,它相对皮带沿带向上滑,受滑动摩擦力f沿带向下,此f作为动力的一部分,因而以较大的加速度沿带加速下滑.当速度增大到带速2m/s后,因相对传送带向下滑,所以滑动摩擦力将改为沿斜面向上,作为物体下滑的一个阻力,因而加速度减小,2m/s这个速度是物体具有不同速度的分界点.第一阶段的受力图如图所示,沿传送带方向和垂直传送带方向应用牛顿第二定律列方程N-mgcosθ=0①,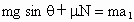 ②. ②.
由①②得 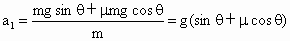
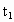 和运动位移 和运动位移 分别为 分别为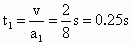 , , . .
第二阶段受力图如图所示,沿带方向和垂直带方向列牛顿第二定律方程  ,N-mgcosθ=0,由此得 ,N-mgcosθ=0,由此得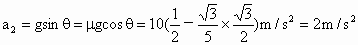 ,第二阶段的位移 ,第二阶段的位移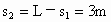 ,由运动学规律 ,由运动学规律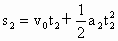 ,代入数值得 ,代入数值得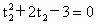 ,解得 ,解得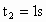 ,所以物体从A运动到B所需的时间t为 ,所以物体从A运动到B所需的时间t为
分过程分析受力及运动情况.
|

练习册系列答案
相关题目
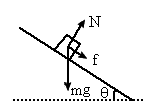

 如图所示,水平传送带逆时针匀速转动,速度为8m/s,A、B为两轮圆心正上方的点,AB=L1=6m,左右两端分别与轨道无缝对接,小物块与轨道左端P碰撞无机械能损失,AP=L2=5m,物块与AP、AB间动摩擦因数均为μ=0.2,物块以一定的初速度v0沿轨道滑上传送带B点,欲使物块可以返回到B点且速度为零,g=10m/s2,则物块的初速度v.不可能的是( )
如图所示,水平传送带逆时针匀速转动,速度为8m/s,A、B为两轮圆心正上方的点,AB=L1=6m,左右两端分别与轨道无缝对接,小物块与轨道左端P碰撞无机械能损失,AP=L2=5m,物块与AP、AB间动摩擦因数均为μ=0.2,物块以一定的初速度v0沿轨道滑上传送带B点,欲使物块可以返回到B点且速度为零,g=10m/s2,则物块的初速度v.不可能的是( ) 如图所示,两轮靠皮带传动(不打滑),绷紧的皮带始终保持 v=3m/s的速度水平地匀速运动.一质量为m=1kg的小物体无初速地放到皮带轮的A处,若物体与皮带的动摩擦因数μ=0.2,AB间距离为L=5.25m.g取10m/s2.
如图所示,两轮靠皮带传动(不打滑),绷紧的皮带始终保持 v=3m/s的速度水平地匀速运动.一质量为m=1kg的小物体无初速地放到皮带轮的A处,若物体与皮带的动摩擦因数μ=0.2,AB间距离为L=5.25m.g取10m/s2. 如图所示,相同的两个轮子A、B半径R1=10cm,用传送带相连.C轮半径R2=5cm,与电动机转轴相连.已知电动机的转速n=300r/min,C轮与A轮间、AB轮与皮带间都不打滑.物体P以v0=1m/s的水平初速度从左端滑上传送带,P与传送带间的动摩擦因数μ=0.57,A、B间距离为2m,求:
如图所示,相同的两个轮子A、B半径R1=10cm,用传送带相连.C轮半径R2=5cm,与电动机转轴相连.已知电动机的转速n=300r/min,C轮与A轮间、AB轮与皮带间都不打滑.物体P以v0=1m/s的水平初速度从左端滑上传送带,P与传送带间的动摩擦因数μ=0.57,A、B间距离为2m,求: ,求物体从A运动到B所需的时间.
,求物体从A运动到B所需的时间.