题目内容
【题目】在地面上固定一块竖直的挡板A,另一块挡板B与水平面成θ角,如图所示。在两块挡板之间放一个质量为m的光滑球体,g取10 m/s2。
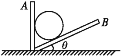
(1)求挡板A对球体的弹力大小,并说明当θ增大时,挡板A对球体的弹力如何变化。
(2)当m=10 kg、θ=37°时,球对挡板B的弹力多大?(sin 37°=0.6,cos 37°=0.8)
【答案】(1)mgtan θ 挡板A对球体的弹力随θ角的增大而增大 (2)125 N
【解析】
对球受力分析,受重力和两个挡板的支持力,然后根据共点力平衡条件列式求解.
(1)对球体受力分析,如图所示
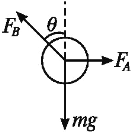
根据力的平衡条件,得:FA=mgtan θ
由上式可得:挡板A对球体的弹力随θ角的增大而增大。
(2)根据平衡条件,得挡板B对球体的弹力为FB![]()
代入数值得:FB=125N
根据牛顿第三定律,球体对挡板B的弹力大小FB'=125 N.

练习册系列答案
相关题目