题目内容
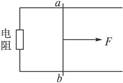
光滑平行金属导轨长L=2m,二导轨间距d=0.5m,轨道平面与水平面的夹角为θ=30°,导轨上端接一阻值为R=0.5 W的电阻,其余电阻不计,轨道所在空间有垂直轨道平面的匀强磁场,磁感应强度B=1T.有一不计电阻的金属棒ab的质量m=0.5kg,放在导轨最上端,如图所示.当ab棒从最上端由静止开始自由下滑,到达底端脱离轨道时,电阻R上产生的热量为Q=1J,求:

(1)当棒的速度为v=2 m/s时,它的加速度是多少?
(2)棒下滑的最大速度是多少?
(3)棒下滑过程中通过电阻R的最大电流是多少?

(1)当棒的速度为v=2 m/s时,它的加速度是多少?
(2)棒下滑的最大速度是多少?
(3)棒下滑过程中通过电阻R的最大电流是多少?
(1) 1 V (2)3 m/s (3)4 A
棒做加速度逐渐减小的变加速运动。
(1)速度为v=2 m/s时,安培力为:FA=BId==1 V
此时的加速度为:a==3 m/s
(2)棒到达底端时速度最大。根据能量守恒定律:mgL sin q=mvm2+Q,
由此可得:vm=4 m/s
(3)速度最大时,感应电动势及感应电流最大。所以有:
Em=Bdv=2 V Im=Em /R=4 A
(1)速度为v=2 m/s时,安培力为:FA=BId==1 V
此时的加速度为:a==3 m/s
(2)棒到达底端时速度最大。根据能量守恒定律:mgL sin q=mvm2+Q,
由此可得:vm=4 m/s
(3)速度最大时,感应电动势及感应电流最大。所以有:
Em=Bdv=2 V Im=Em /R=4 A

练习册系列答案
相关题目




 和
和 水平放置,
水平放置, 间接有阻值为
间接有阻值为 的电阻,导轨相距
的电阻,导轨相距 ,空间有竖直向下的匀强磁场.质量为
,空间有竖直向下的匀强磁场.质量为 ,电阻为
,电阻为 的导体棒
的导体棒 垂直于导轨放置,并接触良好.用平行于
垂直于导轨放置,并接触良好.用平行于 ,经过时间
,经过时间 导体棒
导体棒 .求
.求
 的大小.
的大小.  拉动导体棒
拉动导体棒 .求恒力
.求恒力 。磁场的磁感强度为B,方向垂直纸面向里。现有一段长度为
。磁场的磁感强度为B,方向垂直纸面向里。现有一段长度为 、电阻为
、电阻为 的均匀导体杆MN架在导线框上,开始时紧靠ac,然后沿ab方向以恒定速度v向b端滑动,滑动中始终与ac平行并与导线框保持良好接触。当MN滑过的距离为
的均匀导体杆MN架在导线框上,开始时紧靠ac,然后沿ab方向以恒定速度v向b端滑动,滑动中始终与ac平行并与导线框保持良好接触。当MN滑过的距离为 时,导线ac中的电流是多大?方向如何?
时,导线ac中的电流是多大?方向如何?
 =1m,导线上和导线间接有电阻和电键.已知
=1m,导线上和导线间接有电阻和电键.已知 ,金属杆和裸导线的电阻可忽略不计.若滑杆以大小为v=v'=10m/s的速度沿导线向相反方向滑动,滑动过程中杆始终保持跟导线垂直:
,金属杆和裸导线的电阻可忽略不计.若滑杆以大小为v=v'=10m/s的速度沿导线向相反方向滑动,滑动过程中杆始终保持跟导线垂直: