题目内容
19.在如图所示的电路中,电源的电动势E=3V,内阻r=1Ω,电流表满偏电流为10mA,电流表内阻为7Ω,A,B为接线柱.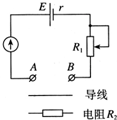
(1)用一条导线把A,B直接连接起来,此时,应把可变电阻R1调节为多少才能使电流表恰好达到满偏?
(2)调至满偏后保持R1阻值不变,在A,B间接入一个电阻R2=300Ω,电流表指针指着多少刻度的位置?
(3)如果把任意电阻R接在A,B间,电流表读数I与R的值有什么关系?
(4)其实,这就是欧姆表的原理,请在如图所示的电流表表盘上选三个位置,对应标出电阻值.通过所标数据可以得到哪些信息?
分析 (1.2)根据闭合电路的欧姆定律即可求出电流表满偏电流时以及电流是5mA时的电阻;
(3.4)欧姆表的工作原理是闭合电路的欧姆定律,根据题意,由欧姆定律可以求出电阻阻值,求出电流表示数与待测电阻阻值间的关系.然后标明刻度即可;
解答 解:(1)满偏时电流大小为10mA,则由闭合电路欧姆定律可得:
I=$\frac{E}{{R}_{内}}$
解得:R内=300Ω;
则R1=300-1-7=292Ω
(2)接入300Ω电阻时电流I′=$\frac{3}{300+300}$=5mA;
故指针指在5mA刻度处;
(3)由闭合电路欧姆定律可得:
I=$\frac{E}{R+{R}_{内}}$=$\frac{3}{300+R}$
(4)电流表“10mA”刻度线标为 0Ω;“5mA”刻度线标为 150Ω;6mA时对应的刻度为200Ω;则说明欧姆表的表盘刻度不均匀;
答:(1)可变电阻R1调节为292Ω时才能使电流表恰好达到满偏;
(2)指针指在5mA刻度处;
(3)把任意电阻R接在A,B间,电流表读数I与R的值关系为I=$\frac{3}{300+R}$
(4)欧姆表的表盘刻度不均匀.
点评 本题考查了求欧姆表的调零电阻阻值、中值电阻阻值、电阻测量值,知道欧姆表的工作原理、应用闭合电路的欧姆定律即可正确解题.

练习册系列答案
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案
相关题目
10.关于地球表面物体受到重力的说法,以下正确的是( )
| A. | 地球上一切物体都受到地球的吸引作用,物体受到的重力,就是地球对它的吸引力 | |
| B. | 重力的大小可以用弹簧测力计测出,物体对弹簧的拉力,就是物体受到的重力 | |
| C. | 物体受到的重力,重力的方向总是竖直向下 | |
| D. | 具有规则几何形状的物体的重心,不一定就在其几何中心上 |
7.如图所示,三颗人造地球卫星的质量满足Ma=Mb<Mc,b与c半径相同,则( )


| A. | 线速度vb=vc>va | |
| B. | 周期Tb=Tc>Ta | |
| C. | b与c的向心加速度大小相等,且大于a的向心加速度 | |
| D. | b所需的向心力最大 |
14.某导体的电流随其两端电压的变化如图,则正确的是( )
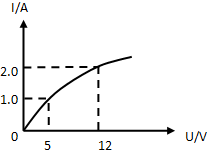

| A. | 导体两端的电压增大,通过导体的电流也增大 | |
| B. | 由图可知,导体两端加5V电压时,导体的电功率为5W | |
| C. | 随着电压的增大,导体的温度升高,导体的电阻不断减小 | |
| D. | 随着电压的增大,导体的温度升高,导体的电阻不断增大 |
4.2014年11月1日,嫦娥五号再入返回飞行试验返回器在内蒙古四子王旗预定区域顺利着陆,这标志着中国探月工程三期再入返回飞行试验获得圆满成功.若该试验器在地球表面的重力为G1,在月球表面的重力为G2,已知地球半径为R1,月球半径R2,地球表面处的重力加速度为g,则下列说法中正确的是( )
| A. | 月球表面处的重力加速度为$\frac{{G}_{1}g}{{G}_{2}}$ | |
| B. | 月球质量与地球质量之比为$\frac{{G}_{2}{{R}_{2}}^{2}}{{G}_{1}{{R}_{1}}^{2}}$ | |
| C. | 该试验器在靠近月球表面轨道上做匀速圆周运动的周期为T=2π$\sqrt{\frac{{G}_{1}{R}_{2}}{{G}_{2}{R}_{1}}}$ | |
| D. | 月球的第一宇宙速度与地球的第一宇宙速度之比为$\sqrt{\frac{{G}_{2}{R}_{2}}{{G}_{1}{R}_{1}}}$ |
11.做匀速圆周运动的物体,其线速度大小为3m/s,角速度为6rad/s,则下列正确的是( )
| A. | 物体运动的向心加速度大小为0.5m/s2 | |
| B. | 物体运动的圆周半径为2m | |
| C. | 物体在1s内发生的位移为3m | |
| D. | 在1s内物体通过的弧长为3m |
8.下列几种情况中,可能发生的是( )
| A. | 位移和加速度反向 | |
| B. | 速度的变化率越大,加速度一定越大 | |
| C. | 速度与加速度反向 | |
| D. | 加速度向右,速度变化的方向向左 |
12.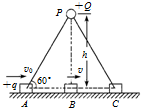 如图,在足够长的绝缘水平直线轨道上,B点正上方h处的P点固定电荷量为+Q的点电荷甲.一质量为m、电荷量为+q的物块乙(可视为质点),从轨道上的A点以初速度v0沿轨道向右运动,当运动到B点时速度为v,到C点时速度正好减为零,已知点电荷甲产生的电场在A点的电势为φ(取无穷远处电势为零),PA连线与水平轨道的夹角为60°.AB=BC,物块乙与水平直线轨道的动摩擦因数为μ,静电力常数为k,由此可得( )
如图,在足够长的绝缘水平直线轨道上,B点正上方h处的P点固定电荷量为+Q的点电荷甲.一质量为m、电荷量为+q的物块乙(可视为质点),从轨道上的A点以初速度v0沿轨道向右运动,当运动到B点时速度为v,到C点时速度正好减为零,已知点电荷甲产生的电场在A点的电势为φ(取无穷远处电势为零),PA连线与水平轨道的夹角为60°.AB=BC,物块乙与水平直线轨道的动摩擦因数为μ,静电力常数为k,由此可得( )
 如图,在足够长的绝缘水平直线轨道上,B点正上方h处的P点固定电荷量为+Q的点电荷甲.一质量为m、电荷量为+q的物块乙(可视为质点),从轨道上的A点以初速度v0沿轨道向右运动,当运动到B点时速度为v,到C点时速度正好减为零,已知点电荷甲产生的电场在A点的电势为φ(取无穷远处电势为零),PA连线与水平轨道的夹角为60°.AB=BC,物块乙与水平直线轨道的动摩擦因数为μ,静电力常数为k,由此可得( )
如图,在足够长的绝缘水平直线轨道上,B点正上方h处的P点固定电荷量为+Q的点电荷甲.一质量为m、电荷量为+q的物块乙(可视为质点),从轨道上的A点以初速度v0沿轨道向右运动,当运动到B点时速度为v,到C点时速度正好减为零,已知点电荷甲产生的电场在A点的电势为φ(取无穷远处电势为零),PA连线与水平轨道的夹角为60°.AB=BC,物块乙与水平直线轨道的动摩擦因数为μ,静电力常数为k,由此可得( )| A. | 物块乙在A点时静电力功率的绝对值为$\frac{3kQq}{8{h}^{2}}$v0 | |
| B. | 物体乙从A点运动到B点克服摩擦力做的功为$\frac{1}{4}$mv02 | |
| C. | 点电荷+Q产生的电场在B点的电势为$\frac{m}{4q}$(v02-2v2)+φ | |
| D. | 物体乙从B点运动到C点过程中电势能减少,到C点时电势能减为零 |
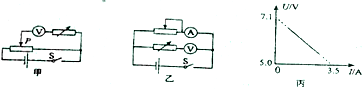 为了测定某迭层电池的电动势(约20-22V)和内电阻(小于2),需要把一个量程为10V的直流电压表接一个固定电阻(用电阻箱代替),改装量程为30V的电压表,然后用伏安法则电源的电动势和内电阻,以下是该实验的操作过程:
为了测定某迭层电池的电动势(约20-22V)和内电阻(小于2),需要把一个量程为10V的直流电压表接一个固定电阻(用电阻箱代替),改装量程为30V的电压表,然后用伏安法则电源的电动势和内电阻,以下是该实验的操作过程: