题目内容
【题目】如图所示，两根等高光滑的四分之一圆弧轨道，半径为r，间距为L，轨道电阻不计，在轨道顶端连有一阻值为R的电阻，整个装置处在一竖直向上的匀强磁场中，磁感应强度为B，现有一根长度稍大于L，电阻为
，质量为m的金属棒从轨道最低位置cd开始，在拉力作用下以速度
向右沿轨道做匀速圆周运动至ab处，求：
（1）初始时刻cd两端的电压；
（2）在该过程中R上产生的热量；
（3）拉力做的功。
【答案】（1）
（2）
（3）
【解析】试题分析：根据法拉第电磁感应定律可得感应电动势，根据串联电路特点求解初始时刻cd两端的电压；分析电路中电磁感应产生的感应电流的特点，求出电流的有效值，根据焦耳定律求解R上产生的热量；由动能定理可得拉力做的功．
（1）刚进入时，根据法拉第电磁感应定律可得感应电动势为
，
根据串联电路特点可知
，解得
（2）导体棒在磁场中做匀速圆周运动，相当于矩形线圈一条边框在磁场中转动，因电磁感应产生的感应电流为正、余弦交流电，所以有
电流的有效值为：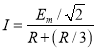 
，所以R上产生的热量为
，
经过的时间为：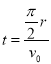 
，解得： 
；
（3）由动能定理可得： 
其中： 
，解得： 
．
练习册系列答案
相关题目
【题目】在《探究力的平行四边形定则》实验时某兴趣小组用如图甲所示的两个力拉弹簧使之伸长至某个位置，并记录，再换一根细线牵引弹簧，使弹簧伸长到同一位置。
（1）本实验采用的科学方法是
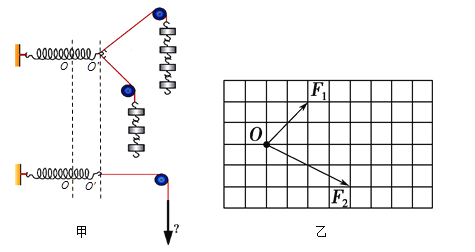
A．理想实验法 | B．等效替代法 |
C．控制变量法 | D．建立物理模型法 |
（2）某同学在坐标纸上画出了如图乙所示的两个已知力F1和F2，图中小正方形的边长表示2 N，则两力的合力F= N，F1与F的夹角分别为θ= 。