题目内容
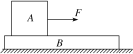
【题目】如图所示,A、B两物块的质量分别为2m和m,静止叠放在水平地面上。A、B间的动摩擦因数为μ,B与地面间的动摩擦因数为![]() μ。设最大静摩擦力等于滑动摩擦力,重力加速度为g。现对A施加一水平恒力F,分别求A与B的加速度:
μ。设最大静摩擦力等于滑动摩擦力,重力加速度为g。现对A施加一水平恒力F,分别求A与B的加速度:
【答案】①当![]() 时,AB静止不动,加速度都为0;
时,AB静止不动,加速度都为0;
②当![]() <F<3μmg时,
<F<3μmg时,![]() ;
;
③当F≥3μmg时,aA=![]() -μg,aB=
-μg,aB=![]() ;
;
【解析】
根据题意可知,B与地面间的最大静摩擦力为:
fBm=![]()
A、B间的最大静摩擦力为:
fABm=2μmg
因此要使B能够相对地面滑动,A对B所施加的摩擦力至少为:
fAB=fBm=![]()
所以,当![]() 时,AB静止不动,加速度都为0
时,AB静止不动,加速度都为0
当A、B将一起向右加速滑动,根据牛顿第二定律可知当满足:
![]() =
=![]()
因为
![]() <fAB<2μmg
<fAB<2μmg
所以
![]() <F<3μmg
<F<3μmg
根据牛顿第二定律可知
AB的加速度
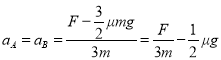
当F≥3μmg时,A、B将以不同的加速度向右滑动,根据牛顿第二定律有:
F-2μmg=2maA
2μmg-![]() =maB
=maB
解得:aA=![]() -μg,aB=
-μg,aB=![]()
综上所述有:
①当![]() 时,AB静止不动,加速度都为0
时,AB静止不动,加速度都为0
②当![]() <F<3μmg时,
<F<3μmg时,![]()
③当F≥3μmg时,aA=![]() -μg,aB=
-μg,aB=![]()

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目