题目内容
16.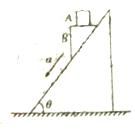 如图所示,质量为M的斜面体放在粗糙的水平面上,两个质量均为m的小物块A和B,在顶端由静止开始沿光滑斜面下滑,下滑过程中A、B保持相对静止,斜面体始终保持静止状态.斜面倾角为θ,下列判断正确的是( )
如图所示,质量为M的斜面体放在粗糙的水平面上,两个质量均为m的小物块A和B,在顶端由静止开始沿光滑斜面下滑,下滑过程中A、B保持相对静止,斜面体始终保持静止状态.斜面倾角为θ,下列判断正确的是( )| A. | B对A的支持力为mg | |
| B. | B对A摩擦力为mgsinθcosθ | |
| C. | 地面对斜面体的支持力为Mg+2mgcos2θ | |
| D. | 地面对斜面体的摩擦力为mgsinθcosθ |
分析 (1)先对AB整体,运用牛顿第二定律求出加速度,再由A,由正交分解法求B对A的摩擦力和支持力.
(2)对C研究,分析受力情况,由平衡条件求地面对C的支持力和摩擦力
解答 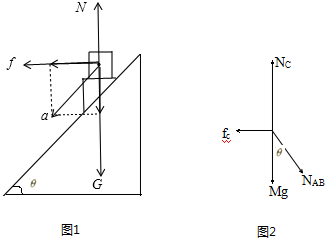 解:A、B整体具有沿斜面向下的加速度,设为加速度为a,由牛顿第二定律可知:
解:A、B整体具有沿斜面向下的加速度,设为加速度为a,由牛顿第二定律可知:
(mA+mB)a=(mA+mB)gsinθ
得:a=gsinθ
将a正交分解为竖直方向分量a1,水平分量a2,如图所示,由于具有水平分量a2,故物体A必受水平向左摩擦力f,A受力如1图所示;
由牛顿第二定律得:
竖直方向上:mAg-N=mAa1…①
水平方向上:f=mAa2…②
斜面与水平方向的夹角为θ,摩擦力与弹力的合力与水平方向夹角为θ,由几何关系得;
a1=asinθ=gsinθsinθ=gsin2θ…③
a2=acosθ=gsinθcosθ…④
得:N=mAg-mAgsin2θ=mAgcos2θ,f=mAgsinθcosθ,故A错误,B正确
C、AB整体对C的压力为 NAB=(mA+mB)gcosθ
分析C的受力情况如图2所示.根据平衡条件得:
NC=Mg+NABcosθ=Mg+(mA+mB)gcos2θ=Mg+2mgcos2θ
fC=NABsinθ=(mA+mB)gsinθcosθ=2mgsinθcosθ,故C正确,D错误
故选:BC
点评 本题AB与C的加速度不同,不好用整体法,可根据隔离法研究,关键要正确分析受力情况,由牛顿第二定律和平衡条件解答

练习册系列答案
 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案
相关题目
6.物体静止在离水平地面一定高出时具有60J的重力势能(以水平地面为重力势能零参考平面),自由下落至某一位置时其重力势能为动能的一半.那么,该过程物体重力势能的减少量是( )
| A. | 20J | B. | 30J | C. | 40J | D. | 60J |
7.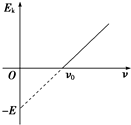 如图所示是某金属在光的照射下产生的光电子的最大初动能Ek与入射光频率ν的关系图象.由图象可知( )
如图所示是某金属在光的照射下产生的光电子的最大初动能Ek与入射光频率ν的关系图象.由图象可知( )
 如图所示是某金属在光的照射下产生的光电子的最大初动能Ek与入射光频率ν的关系图象.由图象可知( )
如图所示是某金属在光的照射下产生的光电子的最大初动能Ek与入射光频率ν的关系图象.由图象可知( )| A. | 该金属的逸出功等于E | |
| B. | 该金属的逸出功等于hν0 | |
| C. | 入射光的频率为3ν0时,产生的光电子的最大初动能为2E | |
| D. | 入射光的频率为$\frac{{v}_{0}}{2}$时,产生的光电子的最大初动能为$\frac{E}{2}$ |
9.某实验小组利用如图a所示的实验装置来探究当小车质量M一定时,物体运动的加速度a与其所受外力F之间的关系.
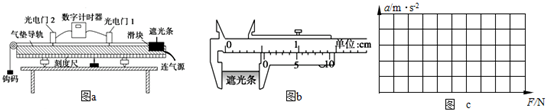
(1)由图中刻度尺读出两个光电门中心之间的距离x=24cm,由图b中游标卡尺测得遮光条的宽度d=0.52 cm.该实验小组在做实验时,将滑块从如图a所示位置由静止释放,由数字计时器可以读出遮光条通过光电门1的时间△t1,遮光条通过光电门2的时间△t2,则滑块经过光电门1时的瞬时速度的表达式v1=$\frac{d}{△{t}_{1}}$,滑块经过光电门2时的瞬时速度的表达式v2=$\frac{d}{△{t}_{2}}$,则滑块的加速度的表达式a=$\frac{{(\frac{d}{△{t}_{2}})}^{2}-{(\frac{d}{△{t}_{1}})}^{2}}{2x}$.(用字母表示)
(2)在本次实验中,实验小组通过改变钩码质量m总共做了8组实验,得到如上表所示的实验数据.请利用表格数据,在如图c所示坐标系中描点做出相应图象.通过分析表中数据后,你得出a-F的图线是否呈线性变化,如果不是请分析其原因:a-F的图线不是一条直线,因为在以增加钩码质量m来增大拉力F的大小时,m越大,M>>m的实验条件越难以保证,所以a-F的图线会出现向F轴方向偏的情况.

(1)由图中刻度尺读出两个光电门中心之间的距离x=24cm,由图b中游标卡尺测得遮光条的宽度d=0.52 cm.该实验小组在做实验时,将滑块从如图a所示位置由静止释放,由数字计时器可以读出遮光条通过光电门1的时间△t1,遮光条通过光电门2的时间△t2,则滑块经过光电门1时的瞬时速度的表达式v1=$\frac{d}{△{t}_{1}}$,滑块经过光电门2时的瞬时速度的表达式v2=$\frac{d}{△{t}_{2}}$,则滑块的加速度的表达式a=$\frac{{(\frac{d}{△{t}_{2}})}^{2}-{(\frac{d}{△{t}_{1}})}^{2}}{2x}$.(用字母表示)
| F(N) | 0.10 | 0.20 | 0.30 | 0.40 | 0.50 | 0.60 | 0.70 | 0.80 |
| a(m•s-2) | 0.06 | 0.11 | 0.18 | 0.26 | 0.30 | 0.36 | 0.40 | 0.43 |
 如图所示,降落伞由于受到水平方向风力而沿着竖直方向成30°角的方向匀速下降,降落伞的人共重600N,求降落伞所受的空气阻力和风力的大小.(不计空气阻力,空气阻力和方向与降落伞运动方向相反)
如图所示,降落伞由于受到水平方向风力而沿着竖直方向成30°角的方向匀速下降,降落伞的人共重600N,求降落伞所受的空气阻力和风力的大小.(不计空气阻力,空气阻力和方向与降落伞运动方向相反)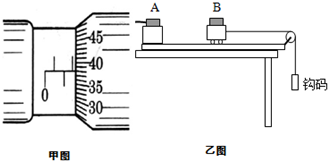 (1)如图所示,甲图中螺旋测微器的读数为1.880mm.
(1)如图所示,甲图中螺旋测微器的读数为1.880mm.
 如图所示,一个质量为10kg的物体,在水推力F的作用下,沿斜面向上匀速运动,已知斜面倾角为37°,物体与斜面间的动摩擦因数为0.5,则水平推力F的大小是200N.
如图所示,一个质量为10kg的物体,在水推力F的作用下,沿斜面向上匀速运动,已知斜面倾角为37°,物体与斜面间的动摩擦因数为0.5,则水平推力F的大小是200N.