Question

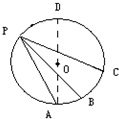如图，PA，PB，PC是竖直圆内三根固定的光滑细杆，P，A，B，C，D点位于同一圆周上，AD为沿竖直方向的一直径，O为圆心．每根杆上都套着一个小圆环，三个滑环都从P点无初速释放．用用t₁、t₂、t₃依次表示滑环滑到A，B，C所用的时间，则（　　）

A．t₃＞t₁＞t₂

B．t₁＞t₂＞t₃

C．t₁＜t₂＜t₃

D．t₁=t₂=t₃

Answer 1

分析：根据“等时圆”的适用条件构造出“等时圆”，作出图象，根据位移之间的关系即可判断运动时间．

解答：解：以P点为最高点，取合适的竖直直径Pe作等时圆，交PB于B，对小滑环，受重力和支持力，将重力沿杆的方向和垂直杆的方向正交分解，根据牛顿第二定律得小滑环做初速为零的匀加速直线运动的加速度为a=gcosθ（θ为杆与竖直方向的夹角）
由图中的直角三角形可知，小滑环的位移S=2Rcosθ
所以t=

2S a

=

4Rcsoθ gcosθ

=

4R g

，t与θ无关，如图所示，显然P到f、B、g、e才是等时的，比较图示位移Pg＞PA，Pf＜PC，故推得t₁＜t₂＜t₃，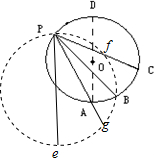
故选：CD

点评：如果不假思考，套用结论，就会落入等时圆”的陷阱，要注意o点不是最高点，难度适中．