题目内容
20．在回旋加速器中，带电粒子在D型盒内经过半个圆周所需要的时间与下列哪些物理量无关？（ ）| A． | 带电粒子的质量和电量 | B． | 带电粒子的速度 | ||
| C． | 加速器的磁感应强度 | D． | 带电粒子运动的轨道半径 |
分析 带电粒子在磁场中受到洛伦兹力而做匀速圆周运动，洛伦兹力提供向心力，由牛顿第二定律和向心力公式列式求半径公式和周期公式．
解答 解：设带电粒子的质量为m，电荷量为q，进入磁场时的速率为v．磁场的磁感应强度为B．
带电粒子在磁场中做匀速圆周运动，洛伦兹力提供向心力，则根据牛顿第二定律得：
qvB=m$\frac{{v}^{2}}{r}$
则得半径：r=$\frac{mv}{qB}$
周期为：T=$\frac{2πr}{v}$=$\frac{2πm}{qB}$，因此经过半个圆周所需要的时间与速度，及轨道半径无关，故BD正确，AC错误；
故选：BD．
点评 对于推导问题，要有必要的假设，步骤要完整，思路要清晰．本题关键抓住洛伦兹力提供向心力进行推导．
练习册系列答案
相关题目
9．有两个共点力，大小分别是3N和5N，则它们的合力大小不可能是（ ）
| A． | 2N | B． | 3N | C． | 5N | D． | 10N |
10．两个同学在做引体向上时，甲同学两手距离与肩同宽，乙同学两手距离大于肩宽，则下列说法正确的是（ ）
| A． | 甲同学更省力 | |
| B． | 乙同学更省力 | |
| C． | 两个同学一样费力 | |
| D． | 若两手挨在一起，比甲、乙同学都省力 |
如图所示为质谱仪的示意图．速度选择器部分的匀强电场场强E，匀强磁场的磁感应强度为B1；偏转分离器的磁感应强度为B2．一质量为m，电荷量为+q的带电微粒进入速度选择器．不计带电微粒的重力．求：
15．实验小组利用如图甲所示的实验装置来探究当合外力一定时，物体运动的加速度与其质量之间的关系．
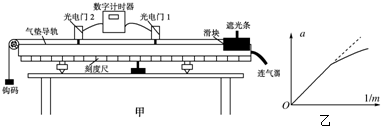
（1）由图甲中刻度尺读出两个光电门中心之间的距离s=50.00cm，通过游标卡尺测得遮光条的宽度d=4.8mm．该实验小组在做实验时，将滑块从图甲所示位置由静止释放，由数字计时器可以读出遮光条通过光电门1的时间△t1和遮光条通过光电门2的时间△t2，则滑块经过光电门1时的瞬时速度的表达式为v1=$\frac{d}{△{t}_{1}}$，滑块的加速度的表达式为$a=\frac{{（\frac{d}{△{t}_{2}}）}^{2}-{（\frac{d}{△{t}_{1}}）}^{2}}{2s}$．（以上表达式均用字母表示）
（2）在本次实验中，实验小组通过改变滑块质量总共做了6组实验，得到如下表所示的实验数据．其中当滑块的质量是350g时，△t1=1.60×10-3s，△t2=1.50×10-3s，
请根据（1）中得到的表达式计算出此时的加速度，并将结果填在下表中相应位置．
（3）实验小组根据实验数据作出了a与$\frac{1}{m}$的图线如右图所示，该图线有一段是弯曲的，试分析图线弯曲的原因：滑块质量较小，不能满足实验条件“滑块质量远大于钩码质量”．
（1）由图甲中刻度尺读出两个光电门中心之间的距离s=50.00cm，通过游标卡尺测得遮光条的宽度d=4.8mm．该实验小组在做实验时，将滑块从图甲所示位置由静止释放，由数字计时器可以读出遮光条通过光电门1的时间△t1和遮光条通过光电门2的时间△t2，则滑块经过光电门1时的瞬时速度的表达式为v1=$\frac{d}{△{t}_{1}}$，滑块的加速度的表达式为$a=\frac{{（\frac{d}{△{t}_{2}}）}^{2}-{（\frac{d}{△{t}_{1}}）}^{2}}{2s}$．（以上表达式均用字母表示）
（2）在本次实验中，实验小组通过改变滑块质量总共做了6组实验，得到如下表所示的实验数据．其中当滑块的质量是350g时，△t1=1.60×10-3s，△t2=1.50×10-3s，
请根据（1）中得到的表达式计算出此时的加速度，并将结果填在下表中相应位置．
| m（g） | a（m/s2） |
| 250 | 1.80 |
| 300 | 1.50 |
| 350 | 1.24 |
| 400 | 1.13 |
| 500 | 0.90 |
| 800 | 0.56 |
9．物体甲的x-t图象和物体乙的v-t图象分别如下图所示，下列说法正确的是（ ） 
| A． | 甲在整个t=6 s时间内来回运动，它通过的总位移为零 | |
| B． | 甲在整个t=6 s时间内通过的位移为4 m | |
| C． | 乙在整个t=6 s时间内来回运动 | |
| D． | 乙在t=3 s时运动方向改变 |