题目内容
【题目】我国计划于2018年择机发射“嫦娥五号”航天器,假设航天器在近月轨道上绕月球做匀速圆周运动,经过时间t(小于绕行周期),运动的弧长为s,航天器与月球中心连线扫过的角度为θ(弧度),引力常量为G,则( )
A. 航天器的轨道半径为![]() B. 航天器的环绕周期为
B. 航天器的环绕周期为![]()
C. 月球的的质量为![]() D. 月球的密度为
D. 月球的密度为![]()
【答案】C
【解析】A项:由题意可知,线速度![]() ,角速度
,角速度![]() ,由线速度与角速度关系
,由线速度与角速度关系![]() 可知,
可知, ![]() ,所以半径为
,所以半径为![]() ,故A错误;
,故A错误;
B项:根据圆周运动的周期公式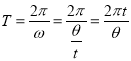 ,故B错误;
,故B错误;
C项:根据万有引力提供向心力可知, ![]() 即
即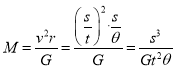 ,故C正确;
,故C正确;
D项:由于不知月球的半径,所以无法求出月球的密度,故D错误;
点晴:解决本题关键将圆周运动的线速度、角速度定义式应用到万有引力与航天中去,由于不知月球的半径,所以无法求出月球的密度。

练习册系列答案
相关题目







