题目内容
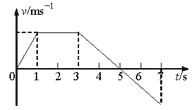
【题目】如图甲所示,一水平传送带沿顺时针方向旋转,在传送带左端A处轻放一可视为质点的小物块,小物块从A端到B端的速度—时间变化规律如图乙所示,t=6s时恰好到B点,则

A. 物块与传送带之间动摩擦因数为μ=0.1
B. AB间距离为24m,小物块在传送带上留下的痕迹是8m
C. 若物块质量m=1kg,物块对传送带做的功为8J
D. 物块速度刚好到4m/s时,传送带速度立刻变为零,物块不能到达B端
【答案】A
【解析】A项:由图乙可知,物块先加速后匀速,且由图乙可知,加速过程的加速度为![]() ,根据牛顿第二定律可知:
,根据牛顿第二定律可知: ![]() ,由以上两式解得:
,由以上两式解得: ![]() ,故A正确;
,故A正确;
B项:AB间距离即为物块在6s内发生的位移,即图乙的面积: ![]() ,故B错误;
,故B错误;
C项:物块对传带只在加速过程中做功,根据公式![]() ,其中
,其中![]() ,
, ![]() ,代入公式中可解得
,代入公式中可解得![]() ,故C错误;
,故C错误;
D项:物块速度刚好到4m/s时,传送带速度立刻变为零,物块由于惯性向前做匀减速直线运动,减速的加速度为![]() ,物块从开始到速度为4m/s时发生的位移为
,物块从开始到速度为4m/s时发生的位移为![]() ,所以物块减速的长度为
,所以物块减速的长度为![]() ,而物块从4m/s减到零发生的位移为
,而物块从4m/s减到零发生的位移为![]() ,所以物块刚好到达B端,故D错误。
,所以物块刚好到达B端,故D错误。
点晴:物块滑上传送带先做匀加速直线运动,当速度达到传送带速度,做匀速直线运动,结合运动学公式和牛顿第二定律求出动摩擦因数,注意判断物块从开始到达到传送带速度时的位移与传送带的长度的比较。

练习册系列答案
相关题目