题目内容
17.猎豹是目前世界上在陆地奔跑速度最快的动物,时速可达110多千米,但不能维持长时间高速奔跑,否则会因身体过热而危及生命.猎豹在一次追击猎物时,经4s速度由静止匀加速到最大,然后匀速运动保持了4s仍没追上猎物,为保护自己它放弃了这次行动,以 3m/s2的加速度匀减速,经10s停下,设此次追捕猎豹始终沿直线运动.求:(1)猎豹奔跑的最大速度可达多少?
(2)猎豹加速时做匀加速运动,则其加速度多大?
(3)猎豹在这次捕猎过程中奔跑的距离是多少?
分析 根据速度时间公式求出猎豹奔跑的最大速度,结合速度时间公式求出加速时的加速度,根据平均速度推论分别求出加速和减速的位移,结合匀速运动的位移,求出总位移.
解答 解:(1)猎豹奔跑的最大速度vm=a2t3=3×10m/s=30m/s.
(2)猎豹加速时的加速度${a}_{1}=\frac{{v}_{m}}{{a}_{1}}=\frac{30}{4}m/{s}^{2}=7.5m/{s}^{2}$.
(3)匀加速运动的位移${x}_{1}=\frac{{v}_{m}}{2}{t}_{1}=\frac{30}{2}×4m=60m$,匀速运动的位移x2=vmt2=30×4m=120m,匀减速运动的位移${x}_{3}=\frac{{v}_{m}}{2}{t}_{3}=\frac{30}{2}×10m=150m$,
则总位移x=x1+x2+x3=60+120+150m=330m.
答:(1)猎豹奔跑的最大速度可达30m/s;
(2)猎豹加速时做匀加速运动,则其加速度为7.5m/s2;
(3)猎豹在这次捕猎过程中奔跑的距离是330m.
点评 解决本题的关键掌握匀变速直线运动的运动学公式和推论,并能灵活运用,有时运用推论求解会使问题更加简捷.

练习册系列答案
相关题目
7. MN是空气与某种液体的分界面.一束红光由空气射到分界面,一部分光线被反射,一部分进入液体中.当入射角是45°时,折射角为30°,如图所示.以下判断正确的是( )
MN是空气与某种液体的分界面.一束红光由空气射到分界面,一部分光线被反射,一部分进入液体中.当入射角是45°时,折射角为30°,如图所示.以下判断正确的是( )
 MN是空气与某种液体的分界面.一束红光由空气射到分界面,一部分光线被反射,一部分进入液体中.当入射角是45°时,折射角为30°,如图所示.以下判断正确的是( )
MN是空气与某种液体的分界面.一束红光由空气射到分界面,一部分光线被反射,一部分进入液体中.当入射角是45°时,折射角为30°,如图所示.以下判断正确的是( )| A. | 反射光线与折射光线的夹角为90° | |
| B. | 该液体对红光的全反射临界角为45° | |
| C. | 在该液体中,红光的传播速度比紫光大 | |
| D. | 当紫光以同样的入射角从空气射到分界面,折射角也是30° |
8.在万有引力常量G已知的情况下,已知下列哪组数据不能计算出地球质量( )
| A. | 地球绕太阳运动的周期及地球离太阳的距离 | |
| B. | 月球绕地球运行的周期及月球绕地球圆周运动的轨道半径 | |
| C. | 人造地球卫星在地面附近绕行的速度和运行周期 | |
| D. | 若不考虑地球自转,已知地球半径和重力加速度 |
5.某同学要测量一节干电池的电动势和内阻,实验器材仅有一个电压表(内阻很大)、一个电阻箱、一个开关和导线若干,该同学按如图1所示电路进行实验,测得的数据如下表所示.

(1)根据表中提供的数据,若利用图象确定电池的电动势和内电阻,则可作以下四项中的A项图象;
A.$U-\frac{U}{R}$B.R-UC.$R-\frac{U}{R}$D.$\frac{1}{R}-U$
(2)根据(1),利用测得的数据,在图2的坐标纸上画出适当的图象;(3)再写出一组有别于(1)中的量作为坐标,使画出的图象为一条直线,所选的量是:$\frac{1}{U}-\frac{1}{R}$或$\frac{1}{R}-\frac{1}{U}$
(4)由做出的图象可知,该电池的电动势E=1.47V(保留三位有效数字),内阻r=0.94Ω
| 实验次数 | 1 | 2 | 3 | 4 | 5 |
| R(Ω) | 2.0 | 4.0 | 6.0 | 8.0 | 10.0 |
| U(V) | 1.00 | 1.19 | 1.27 | 1.31 | 1.35 |
| U/R(A) | 0.50 | 0.30 | 0.21 | 0.16 | 0.13 |

(1)根据表中提供的数据,若利用图象确定电池的电动势和内电阻,则可作以下四项中的A项图象;
A.$U-\frac{U}{R}$B.R-UC.$R-\frac{U}{R}$D.$\frac{1}{R}-U$
(2)根据(1),利用测得的数据,在图2的坐标纸上画出适当的图象;(3)再写出一组有别于(1)中的量作为坐标,使画出的图象为一条直线,所选的量是:$\frac{1}{U}-\frac{1}{R}$或$\frac{1}{R}-\frac{1}{U}$
(4)由做出的图象可知,该电池的电动势E=1.47V(保留三位有效数字),内阻r=0.94Ω
12.下列关于功率的说法,错误的是( )
| A. | 功率是反映做功快慢的物理量 | |
| B. | 据公式P=$\frac{W}{t}$,求出的是力F在t时间内做功的平均功率 | |
| C. | 据公式P=Fv可知,汽车的运动速率增大,牵引力一定减小 | |
| D. | 据公式P=Fvcosα,若知道运动物体在某一时刻的速度大小,该时刻作用力F的大小以及二者之间的夹角.便可求出该段时间内F做功的功率 |
7. 如图所示,质量为m和2m的两个小球固定在长为2l的轻杆两端,杆的中点是一水平转轴O,系统可在竖直面内无摩擦转动,空气阻力不计.若从杆处于水平位置由静止释放系统,系统转过90°的过程中,以下说法正确的是(重力加速度g已知)( )
如图所示,质量为m和2m的两个小球固定在长为2l的轻杆两端,杆的中点是一水平转轴O,系统可在竖直面内无摩擦转动,空气阻力不计.若从杆处于水平位置由静止释放系统,系统转过90°的过程中,以下说法正确的是(重力加速度g已知)( )
 如图所示,质量为m和2m的两个小球固定在长为2l的轻杆两端,杆的中点是一水平转轴O,系统可在竖直面内无摩擦转动,空气阻力不计.若从杆处于水平位置由静止释放系统,系统转过90°的过程中,以下说法正确的是(重力加速度g已知)( )
如图所示,质量为m和2m的两个小球固定在长为2l的轻杆两端,杆的中点是一水平转轴O,系统可在竖直面内无摩擦转动,空气阻力不计.若从杆处于水平位置由静止释放系统,系统转过90°的过程中,以下说法正确的是(重力加速度g已知)( )| A. | 该过程杆中弹力对m做正功 | |
| B. | 该过程系统机械能守恒,2m的小球机械能也守恒 | |
| C. | 系统转过90°,杆处于竖直方向时,两小球速度均为v=$\sqrt{\frac{2gl}{3}}$ | |
| D. | 系统转过90°,杆处于竖直方向时,轴O对杆的作用力大小为4mg,方向竖直向上 |
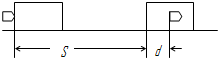 如图所示,一木块放在光滑水平面上,一子弹水平射入木块中,射入深度为d,平均阻力为f.设木块离原点s远时开始匀速前进,木块增加的动能=fs;子弹损失的动能=f(s+d).
如图所示,一木块放在光滑水平面上,一子弹水平射入木块中,射入深度为d,平均阻力为f.设木块离原点s远时开始匀速前进,木块增加的动能=fs;子弹损失的动能=f(s+d).