题目内容
【题目】如图所示,质量为m1=20kg的物体A经一轻质弹簧与下方斜面上的质量为m2=20kg的物体B相连,弹簧的劲度系数为 k=50N/m,斜面是光滑的,其倾角为θ=30°。A、B都处于静止状态。一条不可伸长的轻绳绕过轻滑轮,一端连物体 A,另一端连质量为m3=34.7kg的物体C。物体C又套在光滑竖直固定 的细杆上,开始时各段绳都处于伸直状态,但没绷紧,OC段绳是水平的,OC段的距离d=6m,A上方的一段绳沿斜面方向。现在静止释放物体C,已知它恰好能使B离开挡板但不继续上升。(结果保留一位有效数字)
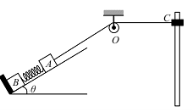
(1)当B刚离开挡板时,物体A沿着斜面上滑的距离L;
(2)当B刚离开挡板时,A的速度 v1大小是多少?
【答案】(1)4m (2)8m/s
【解析】
试题分析:(1)开始时,A、B静止,设弹簧压缩量为x1,有:kx1=m1gsinθ
设B刚要离开挡板时弹簧的伸长量为x2,则有:kx2=m2gsinθ
由几何关系有:L=x1+x2;
解得A上升的距离为:![]()
(2)设第一次运动过程中,弹簧的弹性势能的变化为△Ep,C下降的高度为:![]()
对A、B、C弹簧和地球组成的系统,由能量守恒定律得:m3gh=m1gLsinθ+△Ep
在第二次运动过程中,当B刚离开挡板时,设A速度为v1,C速度为v2
对A、B、C弹簧和地球组成的系统使用能量守恒定律,由题意得:
M3gh=m1gLsinθ +![]() m1v12+
m1v12+![]() m3v22
m3v22
又 v1=v2cos37°
联立解得:v1=8 m/s

练习册系列答案
相关题目