题目内容
8.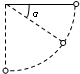 如图所示,一端固定的绳,另一端系一球,现将绳拉至水平位置将球由静止释放.若不计空气阻力,设最低点重力势能为0,当球摆至动能为重为势能2倍处时,求绳与水平方向夹角α.
如图所示,一端固定的绳,另一端系一球,现将绳拉至水平位置将球由静止释放.若不计空气阻力,设最低点重力势能为0,当球摆至动能为重为势能2倍处时,求绳与水平方向夹角α.
分析 通过受力分析可知,小球受到重力和绳子的拉力的作用,只有重力做功,机械能守恒,向下运动的过程中重力势能转化为动能,势能减小,动能增大,再根据动能为重为势能2倍处时的特点即可求出,
解答 解:小球向下运动的过程中重力势能转化为动能,势能减小,动能增大,设最低点重力势能为0,小球开始时的重力势能为:mgl.
当球摆至动能为重为势能2倍处时,则满足:EK=2EP,同时:EK+EP=mgl,EP=mgl(1-sinα)
所以得:sinα=$\frac{2}{3}$,即α=41.8°
答:当球摆至动能为重为势能2倍处时,绳与水平方向夹角α是41.8°.
点评 在题目中虽然小球除了受到重力的作用之外还受到绳的拉力的作用,但是在整个过程中绳的拉力不做功,只有重力做功,机械能守恒.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
13.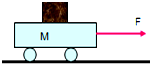 在光滑水平面上以水平恒力F拉动小车和木块,一起做无相对滑动的加速运动,若小车质量为M,木块质量为m,木块和小车间的动摩擦因数为μ.则小车与物块之间的摩擦力大小为$\frac{mF}{M+m}$.
在光滑水平面上以水平恒力F拉动小车和木块,一起做无相对滑动的加速运动,若小车质量为M,木块质量为m,木块和小车间的动摩擦因数为μ.则小车与物块之间的摩擦力大小为$\frac{mF}{M+m}$.
 在光滑水平面上以水平恒力F拉动小车和木块,一起做无相对滑动的加速运动,若小车质量为M,木块质量为m,木块和小车间的动摩擦因数为μ.则小车与物块之间的摩擦力大小为$\frac{mF}{M+m}$.
在光滑水平面上以水平恒力F拉动小车和木块,一起做无相对滑动的加速运动,若小车质量为M,木块质量为m,木块和小车间的动摩擦因数为μ.则小车与物块之间的摩擦力大小为$\frac{mF}{M+m}$.
17. 如图所示,质量分别为m1和m2的木块之间用轻弹簧相连,在拉力F的作用下,一起以加速度g竖直向上做匀加速直线运动,某时刻突然撤去拉力F,设此时m1和m2的加速度分别为aA和aB,规定竖直向上为正方向,则( )
如图所示,质量分别为m1和m2的木块之间用轻弹簧相连,在拉力F的作用下,一起以加速度g竖直向上做匀加速直线运动,某时刻突然撤去拉力F,设此时m1和m2的加速度分别为aA和aB,规定竖直向上为正方向,则( )
 如图所示,质量分别为m1和m2的木块之间用轻弹簧相连,在拉力F的作用下,一起以加速度g竖直向上做匀加速直线运动,某时刻突然撤去拉力F,设此时m1和m2的加速度分别为aA和aB,规定竖直向上为正方向,则( )
如图所示,质量分别为m1和m2的木块之间用轻弹簧相连,在拉力F的作用下,一起以加速度g竖直向上做匀加速直线运动,某时刻突然撤去拉力F,设此时m1和m2的加速度分别为aA和aB,规定竖直向上为正方向,则( )| A. | aA=-g,aB=-$\frac{2{m}_{1}}{{m}_{2}}$g | B. | aA=g,aB=-$\frac{2{m}_{2}+{m}_{1}}{{m}_{1}}$g | ||
| C. | aA=g,aB=-$\frac{2{m}_{1}+{m}_{2}}{{m}_{2}}$g | D. | aA=$\frac{{m}_{1}}{{m}_{1}+{m}_{2}}$g,aB=$\frac{{m}_{2}}{{m}_{1}+{m}_{2}}$g |
18.一木箱放在水平地面上,下列关于木箱和地面所受弹力的叙述中 正确的是( )
| A. | 地面受到向下的弹力,是因为木箱发生了弹性形变;木箱受到了向上的弹力,是因为地面也发生了形变 | |
| B. | 地面受到向下的弹力,是因为地面发生了弹性形变;木箱没有发生形变,所以木箱不受弹力 | |
| C. | 地面受到向下的弹力,是因为地面发生了弹性形变;木箱受到了向上的弹力,是因为木箱也发生了形变 | |
| D. | 以上说法都不正确 |
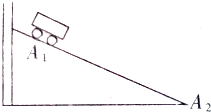 现要验证“当质量一定时,物体运动的加速度与它所受的合外力成正比”这一物理规律.
现要验证“当质量一定时,物体运动的加速度与它所受的合外力成正比”这一物理规律.