题目内容
13. 如图a所示,质量为m的物体静止在倾角为θ的平板上,当θ从0缓慢增大到90°的过程中,物体所受摩擦力Ff与θ的关系如图b所示,已知物球体始终没有脱离平板,物体与平板间的动摩擦因数为0.75.最大静摩擦力与滑动摩擦力相等,重力加速度为g,则( )
如图a所示,质量为m的物体静止在倾角为θ的平板上,当θ从0缓慢增大到90°的过程中,物体所受摩擦力Ff与θ的关系如图b所示,已知物球体始终没有脱离平板,物体与平板间的动摩擦因数为0.75.最大静摩擦力与滑动摩擦力相等,重力加速度为g,则( )| A. | O-q段图象可能是直线 | B. | q-$\frac{π}{2}$段图象可能是直线 | ||
| C. | $p=\frac{3mg}{5}$ | D. | $q=\frac{π}{4}$ |
分析 半球体受重力、支持力和摩擦力,开始时不滑动,是静摩擦力,根据平衡条件列式求解静摩擦力表达式分析;滑动后是滑动摩擦力,根据滑动摩擦定律列式分析.
解答 解:ABD、θ在0-37°之间时,Ff是静摩擦力,大小为mgsinθ;
θ在37°-90° 之间时,Ff是滑动摩擦力,大小为μmgcosθ;
综合以上分析得其Ff与θ关系如图中实线所示,故A、B错误;
半圆体在平板上恰好开始滑动的临界条件是:
mgsinθ=μmgcosθ,
故有:μ=tanθ=0.75,
解得:θ=37°,
即q=37°,故D错误;
C、当θ=37°时,Ff=mgsin37°=$\frac{3mg}{5}$,即p=$\frac{3mg}{5}$,故C正确.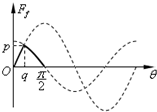
故选:C.
点评 本题关键是受力分析后要能够区分是滑动摩擦力还是静摩擦力,然后结合平衡条件和滑动摩擦定律列式分析,基础题目.

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
3.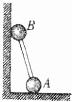 如图,两球通过轻杆连接,A球在水平面上,B球紧靠竖直墙壁,开始时,控制杆与水平方向成53°角,球A的质量为0.1kg,球B的质量为0.2kg,杆长1m,释放后,A球向右滑动,B球沿竖直墙壁下滑,直至杆与水平方向夹角为30°,不计一切摩擦及球的大小,则( )
如图,两球通过轻杆连接,A球在水平面上,B球紧靠竖直墙壁,开始时,控制杆与水平方向成53°角,球A的质量为0.1kg,球B的质量为0.2kg,杆长1m,释放后,A球向右滑动,B球沿竖直墙壁下滑,直至杆与水平方向夹角为30°,不计一切摩擦及球的大小,则( )
 如图,两球通过轻杆连接,A球在水平面上,B球紧靠竖直墙壁,开始时,控制杆与水平方向成53°角,球A的质量为0.1kg,球B的质量为0.2kg,杆长1m,释放后,A球向右滑动,B球沿竖直墙壁下滑,直至杆与水平方向夹角为30°,不计一切摩擦及球的大小,则( )
如图,两球通过轻杆连接,A球在水平面上,B球紧靠竖直墙壁,开始时,控制杆与水平方向成53°角,球A的质量为0.1kg,球B的质量为0.2kg,杆长1m,释放后,A球向右滑动,B球沿竖直墙壁下滑,直至杆与水平方向夹角为30°,不计一切摩擦及球的大小,则( )| A. | 在滑动过程中AB两球速度大小始终相等 | |
| B. | AB两球和杆组成的系统机械能守恒 | |
| C. | 最后A球的速度大小为2m/s | |
| D. | 最后B球的速度大小为$\frac{6\sqrt{7}}{7}$m/s |
18.下列事例中有关速度的说法,正确的是( )
| A. | 某高速公路上的限速为110 km/h,指的是瞬时速度 | |
| B. | 汽车速度计上显示80 km/h,指的是平均速度 | |
| C. | 火车从济南到北京的速度约为220 km/h,指的是瞬时速度 | |
| D. | 子弹以900 km/h的速度从枪口射出,指的是瞬时速度 |
5.一半径为R的绝缘球壳上均匀地带有电荷量为+Q的电荷,另一电荷量为+q的点电荷放在球心O上.由于对称性,点电荷受力为零.现在球壳上挖去半径为r(r?R)的一个很小的圆孔,则此时置于球心处的点电荷( )
| A. | 受力大小为零 | |
| B. | 受力大小为$\frac{kqQ}{{R}^{2}}$,方向由圆孔指向球心 | |
| C. | 受力大小为$\frac{kqQ{r}^{2}}{4{R}^{4}}$,方向由圆孔指向球心 | |
| D. | 受力大小为$\frac{kqQ{r}^{2}}{4{R}^{4}}$,方向由球心指向圆孔 |
2.在竖直平面内做匀速圆周运动的物体,在运动过程中没有发生变化的物理是( )
| A. | 速度 | B. | 加速度 | C. | 合外力 | D. | 角速度 |
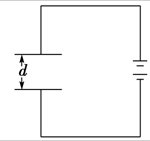 将电容C=3.0×10-10F,两极板间距离d=1.20×10-3m的平行板电容器始终接在电压为10V的直流电源上.如图所示,取g=10m/s2.
将电容C=3.0×10-10F,两极板间距离d=1.20×10-3m的平行板电容器始终接在电压为10V的直流电源上.如图所示,取g=10m/s2.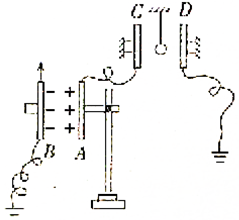 某同学在研究平行板电容器的决定因素实验中,由于手边没有静电计,就再用一个平行板电容器CD作为静电计使用,如图所示,将该平行板电容器沿竖直方向固定在绝缘支架上,并在极板间悬挂一个带正电的小球,现使AB金属板带上等量的异种电荷,B板和D板分别接地,并使A板与C板相连,则:
某同学在研究平行板电容器的决定因素实验中,由于手边没有静电计,就再用一个平行板电容器CD作为静电计使用,如图所示,将该平行板电容器沿竖直方向固定在绝缘支架上,并在极板间悬挂一个带正电的小球,现使AB金属板带上等量的异种电荷,B板和D板分别接地,并使A板与C板相连,则: