题目内容
如图,斜面体C质量为M足够长,始终静止在水平面上,一质量为m的长方形木板A上表面光滑,木板A获得初速度v后恰好能沿斜面匀速下滑,当木板A匀速下滑时将一质量也为m的滑块B轻轻放在木板A表面上,当滑块B在木板A上滑动时,下列说法正确的是( )
A.滑块B的动量为0.5mv时,木板A和滑块B的加速度大小相等
B.滑块B的动量为0.5mv时,斜面体对水平面的压力大小为(M+2m)g
C.滑块B的动量为1.5mv时,木板A的动量为0.5mv
D.滑块B的动量为1.5mv时,水平面对斜面体的摩擦力向右
【答案】分析:对A、B进行受力分析求出AB的加速度,再结合动量守恒定律即可求解.
解答:解:A、A匀速运动,则mgsinθ=μmgcosθ,
放上B物体后,maA=2mgμcosθ-mgsinθ
解得:aA=gsinθ
对B进行受力分析根据牛顿第二定律得:
maB=mgsinθ,
解得:aB=gsinθ
所以A正确;
B、以物块AB为研究对象,其合外力为零符合动量守恒,满足mv=mv1+mv2,滑块B的动量为0.5mv时,木板A的动量为0.5mv,此时A沿斜面向下运动,所以A对C的滑动摩擦力方向沿斜面向下,
对C进行受力分析:如图所示,合力为零.
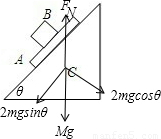
则有:FN=Mg+2mg,故B正确;
C、以物块AB为研究对象,其合外力为零符合动量守恒,满足mv=mv1+mv2,滑块B的动量为1.5mv时,木板A的动量为-0.5mv,故C错误;
D、由C分析可知:滑块B的动量为1.5mv时,木板A的动量为-0.5mv,此时A沿斜面向上运动,A受到的滑动摩擦力方向沿斜面向下,所以C受到A的滑动摩擦力方向沿斜面向上,C仍静止,受力平衡,则水平面对斜面体的摩擦力向左,故D错误.
故选AB
点评:本题考查牛顿定律、动量守恒的应用,关键是对物体的受力分析,难度较大.
解答:解:A、A匀速运动,则mgsinθ=μmgcosθ,
放上B物体后,maA=2mgμcosθ-mgsinθ
解得:aA=gsinθ
对B进行受力分析根据牛顿第二定律得:
maB=mgsinθ,
解得:aB=gsinθ
所以A正确;
B、以物块AB为研究对象,其合外力为零符合动量守恒,满足mv=mv1+mv2,滑块B的动量为0.5mv时,木板A的动量为0.5mv,此时A沿斜面向下运动,所以A对C的滑动摩擦力方向沿斜面向下,
对C进行受力分析:如图所示,合力为零.

则有:FN=Mg+2mg,故B正确;
C、以物块AB为研究对象,其合外力为零符合动量守恒,满足mv=mv1+mv2,滑块B的动量为1.5mv时,木板A的动量为-0.5mv,故C错误;
D、由C分析可知:滑块B的动量为1.5mv时,木板A的动量为-0.5mv,此时A沿斜面向上运动,A受到的滑动摩擦力方向沿斜面向下,所以C受到A的滑动摩擦力方向沿斜面向上,C仍静止,受力平衡,则水平面对斜面体的摩擦力向左,故D错误.
故选AB
点评:本题考查牛顿定律、动量守恒的应用,关键是对物体的受力分析,难度较大.

练习册系列答案
相关题目
 如图,斜面体C质量为M足够长,始终静止在水平面上,一质量为m的长方形木板A上表面光滑,木板A获得初速度v0后恰好能沿斜面匀速下滑,当木板A匀速下滑时将一质量也为m的滑块B轻轻放在木板A表面上,当滑块B在木板A上滑动时,下列不正确的是( )
如图,斜面体C质量为M足够长,始终静止在水平面上,一质量为m的长方形木板A上表面光滑,木板A获得初速度v0后恰好能沿斜面匀速下滑,当木板A匀速下滑时将一质量也为m的滑块B轻轻放在木板A表面上,当滑块B在木板A上滑动时,下列不正确的是( )

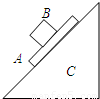 如图,斜面体C质量为M足够长,始终静止在水平面上,一质量为m的长方形木板A上表面光滑,木板A获得初速度v后恰好能沿斜面匀速下滑,当木板A匀速下滑时将一质量也为m的滑块B轻轻放在木板A表面上,当滑块B在木板A上滑动时,下列不正确的是( )
如图,斜面体C质量为M足够长,始终静止在水平面上,一质量为m的长方形木板A上表面光滑,木板A获得初速度v后恰好能沿斜面匀速下滑,当木板A匀速下滑时将一质量也为m的滑块B轻轻放在木板A表面上,当滑块B在木板A上滑动时,下列不正确的是( )