题目内容
如图,斜面体C质量为M,斜面足够长,始终静止在水平面上,一质量为m的长方形木板A,上表面光滑,木板A获得初速度v0后正好能沿着斜面匀速下滑,当木板A匀速下滑时将一质量也为m的滑块B轻轻放在木块A表面,当滑块B在木块A上滑动时( )
A.滑块B的动量为(1/2)mv0时,木块A和滑块B速度大小相等
B.滑块B的动量为(1/2)mv0时,斜面体对水平面压力大小为(M+
C.滑块B的动量为(3/2)mv0时,木板A的动量为(-1/2)mv0
D.滑块B的动量为(3/2)mv0时,水平面对斜面体的摩擦力向左
ABD 【解析】木板A获得初速度v0后正好能沿着斜面匀速下滑,则μ=tanθ.对AB系统,沿斜面方向受力平衡,即2mgsinθ-μ·2mgcosθ=0,动量守恒,因此有mv0=m![]() +mv′,v′=
+mv′,v′=![]() ,木板速度与滑块相等,A正确;由于A,B系统所受合外力为零,系统加速度为零,斜面对地面的压力等于A,B,C总重力,B正确;木板A速度减小到零后滑动摩擦力变为静摩擦力,A静止,B可继续下滑,C错;滑块B的动量为(3/2)mv0时,木板静止,B具有向左的加速度分量,因此系统必受到向左的合外力,即水平面对斜面的静摩擦力向左,D正确.考查牛顿第二定律、物体的平衡条件、动量守恒及摩擦力变化等,较难.
,木板速度与滑块相等,A正确;由于A,B系统所受合外力为零,系统加速度为零,斜面对地面的压力等于A,B,C总重力,B正确;木板A速度减小到零后滑动摩擦力变为静摩擦力,A静止,B可继续下滑,C错;滑块B的动量为(3/2)mv0时,木板静止,B具有向左的加速度分量,因此系统必受到向左的合外力,即水平面对斜面的静摩擦力向左,D正确.考查牛顿第二定律、物体的平衡条件、动量守恒及摩擦力变化等,较难.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
 如图,斜面体C质量为M足够长,始终静止在水平面上,一质量为m的长方形木板A上表面光滑,木板A获得初速度v0后恰好能沿斜面匀速下滑,当木板A匀速下滑时将一质量也为m的滑块B轻轻放在木板A表面上,当滑块B在木板A上滑动时,下列不正确的是( )
如图,斜面体C质量为M足够长,始终静止在水平面上,一质量为m的长方形木板A上表面光滑,木板A获得初速度v0后恰好能沿斜面匀速下滑,当木板A匀速下滑时将一质量也为m的滑块B轻轻放在木板A表面上,当滑块B在木板A上滑动时,下列不正确的是( )
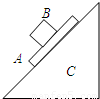 如图,斜面体C质量为M足够长,始终静止在水平面上,一质量为m的长方形木板A上表面光滑,木板A获得初速度v后恰好能沿斜面匀速下滑,当木板A匀速下滑时将一质量也为m的滑块B轻轻放在木板A表面上,当滑块B在木板A上滑动时,下列不正确的是( )
如图,斜面体C质量为M足够长,始终静止在水平面上,一质量为m的长方形木板A上表面光滑,木板A获得初速度v后恰好能沿斜面匀速下滑,当木板A匀速下滑时将一质量也为m的滑块B轻轻放在木板A表面上,当滑块B在木板A上滑动时,下列不正确的是( )