题目内容
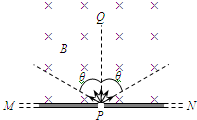如图所示，MN是一荧光屏，当带电粒子打到荧光屏上时，荧光屏能够发光．MN的上方有磁感应强度为B的匀强磁场，磁场方向垂直纸面向里．P为屏上的一小孔，PQ与MN垂直．一群质量为m、带电荷量q的粒子（不计重力），以相同的速率v，从P处沿垂直于磁场方向射入磁场区域，且分布在与PQ夹角为θ的范围内，不计粒子间的相互作用．则以下说法正确的是（ ）分析：一群质量为m、带电荷量q的粒子（不计重力），以相同的速率v从小孔P处沿垂直于磁场方向入射，在洛伦兹力作用下做匀速圆周运动．由于入射角度的不同，导致打到荧光屏上的远近不一．最终在P点一侧出现一个条形亮线．画出轨迹，根据洛伦兹力提供向心力和几何关系求解．
解答：解：A、B：一群质量为m、带电荷量q的粒子（不计重力），以相同的速率v从小孔P处沿垂直于磁场方向入射，则不可能在荧光屏上出现圆形亮斑，也不会出现半圆形亮斑，故A、B均错误；
C、D：一群质量为m、带电荷量q的粒子（不计重力），以相同的速率v从小孔P处沿垂直于磁场方向入射，在荧光屏上将出现一个条形亮线，其长度是由离P点最远与最近的距离之差．而最远的距离是轨迹刚好完成半个圆，则距离为2R，最近的距离是粒子沿θ入射所对应的一段圆弧，其距离为2Rcosθ，所以最远与最近的距离之差为
（1-cosθ），故C正确、D错误．
故选C．
C、D：一群质量为m、带电荷量q的粒子（不计重力），以相同的速率v从小孔P处沿垂直于磁场方向入射，在荧光屏上将出现一个条形亮线，其长度是由离P点最远与最近的距离之差．而最远的距离是轨迹刚好完成半个圆，则距离为2R，最近的距离是粒子沿θ入射所对应的一段圆弧，其距离为2Rcosθ，所以最远与最近的距离之差为
| 2mv |
| qB |
故选C．
点评：根据题意会画出各种情况的运动轨迹，结合圆的特性及几何关系可求出结果．本题有一定的难度，要出运动轨迹是关键．
练习册系列答案
相关题目
（2011?重庆模拟）如图所示，MN是一荧光屏，当带电粒子打到荧光屏上时，荧光屏能够发光．MN的上方有磁感应强度为B的匀强磁场，磁场方向垂直纸面向里．P为屏上的一小孔，PQ与MN垂直．一群质量为m、带电荷量都为q的正负两种粒子（不计重力），以相同的速率v，从小孔P处沿垂直于磁场且与PQ夹角为θ的范围内向各个方向射入磁场区域，不计粒子间的相互作用．则以下说法正确的是（ ）
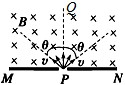如图所示，MN是一荧光屏，当带电粒子打到荧光屏上时，荧光屏能够发光．MN的上方有磁感应强度为B的匀强磁场，磁场方向垂直纸面向里．P为屏上的一小孔，PQ与MN垂直．一群质量为m、带电荷量都为q的正负两种粒子（不计重力），以相同的速率v，从小孔P处沿垂直于磁场且与PQ夹角为θ的范围内向各个方向射入磁场区域，不计粒子间的相互作用．则以下说法正确的是（ ）A、在荧光屏上将出现一个圆形亮环，其外半径为
| ||||
B、在荧光屏上P点两侧将出现两个相等长度条形亮线，其长度为
| ||||
C、粒子运动过程中到荧光屏MN的最大距离为
| ||||
D、在荧光屏上P点两侧将出现两个相等长度条形亮线，其长度为
|
