题目内容
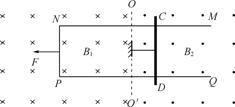
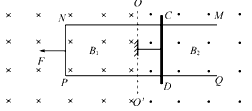
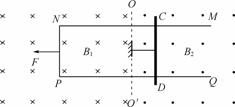
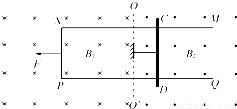
如图所示存在范围足够大的磁场区,虚线OO′为磁场边界,左侧为竖直向下的匀强磁场,磁感应强度为B1,右侧为竖直向上的磁感应强度为B2的匀强磁场区,B1=B2=B.有一质量为m且足够长的U形金属框架MNPQ平放在光滑的水平面上,框架跨过两磁场区,磁场边界OO′与框架的两平行导轨MN、PQ垂直,两导轨相距L,一质量也为m的金属棒垂直放置在右侧磁场区光滑的水平导轨上,并用一不可伸长的绳子拉住,绳子能承受的最大拉力是F,超过F绳子会自动断裂,已知棒的电阻是R,导轨电阻不计,t=0时刻对U形金属框架施加水平向左的拉力F让其从静止开始做加速度为a的匀加速直线运动.(1)求在绳未断前U形金属框架做匀加速运动t时刻水平拉力F的大小;绳子断开后瞬间棒的加速度.
(2)若在绳子断开的时刻立即撤去拉力F,框架和导体棒将怎样运动,求出它们的最终状态的速度.
(3)在(2)的情景下,求出撤去拉力F后棒上产生的电热和通过导体棒的电量.
【答案】分析:(1)根据法拉第电磁感应定律和牛顿第二定律求解.
(2)以后框架减速,棒向右加速,当两者速度大小相等时回路磁通量不再变化,一起匀速运动.由于框架和棒都是受安培力作用,且质量相等,所以任意时刻加速度大小相等.
(3)去拉力F后系统动能减少等于回路消耗电能,根据能量守恒定律求解.
解答:解:(1)t=0时刻对U形金属框架施加水平向左的拉力F让其从静止开始做加速度为a的匀加速直线运动.
对框架 v=at
感应电动势E=BLv=BLat
安培力 F安=BIL=
根据牛顿第二定律得
F-F安=ma
F=F安+ma=ma+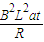
绳子断开时刻绳子拉力 F=F安
棒的加速度a=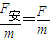
(2)绳子断裂时刻F=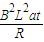
t=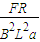
框架速度v=at=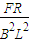
以后框架减速,棒向右加速,当两者速度大小相等时回路磁通量不再变化,一起匀速运动.由于框架和棒都是受安培力作用,且质量相等,所以任意时刻加速度大小相等,相等时间内速度变化的大小也相等,最终速度都是v,
v-v=v-0,
v=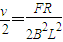
框架向左匀速,棒向右匀速.
(3)撤去拉力F后系统动能减少等于回路消耗电能,即棒上产生电热
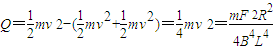
对棒 F安=BIL=ma
a=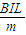
△t时间速度变化△v=a△t=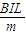 △t=
△t=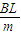 △q
△q
速度由零增加到v过程
v=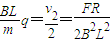
q=
答:(1)在绳未断前U形金属框架做匀加速运动t时刻水平拉力F的大小是ma+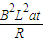 ,绳子断开后瞬间棒的加速度是
,绳子断开后瞬间棒的加速度是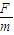 .
.
(2)若在绳子断开的时刻立即撤去拉力F,框架和导体棒将怎样运动,它们的最终状态是框架向左匀速,棒向右匀速.
(3)在(2)的情景下,撤去拉力F后棒上产生的电热是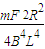 ,通过导体棒的电量是
,通过导体棒的电量是 .
.
点评:本题考查了法拉第电磁感应定律、牛顿第二定律、能量守恒定律等多个知识点,要注意的是该题中框架NP和金属棒所在的磁场方向相反,从而所受安培力方向相同.
(2)以后框架减速,棒向右加速,当两者速度大小相等时回路磁通量不再变化,一起匀速运动.由于框架和棒都是受安培力作用,且质量相等,所以任意时刻加速度大小相等.
(3)去拉力F后系统动能减少等于回路消耗电能,根据能量守恒定律求解.
解答:解:(1)t=0时刻对U形金属框架施加水平向左的拉力F让其从静止开始做加速度为a的匀加速直线运动.
对框架 v=at
感应电动势E=BLv=BLat
安培力 F安=BIL=

根据牛顿第二定律得
F-F安=ma
F=F安+ma=ma+
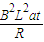
绳子断开时刻绳子拉力 F=F安
棒的加速度a=
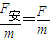
(2)绳子断裂时刻F=
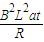
t=
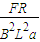
框架速度v=at=
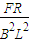
以后框架减速,棒向右加速,当两者速度大小相等时回路磁通量不再变化,一起匀速运动.由于框架和棒都是受安培力作用,且质量相等,所以任意时刻加速度大小相等,相等时间内速度变化的大小也相等,最终速度都是v,
v-v=v-0,
v=
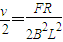
框架向左匀速,棒向右匀速.
(3)撤去拉力F后系统动能减少等于回路消耗电能,即棒上产生电热
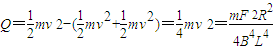
对棒 F安=BIL=ma
a=
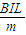
△t时间速度变化△v=a△t=
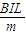 △t=
△t=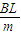 △q
△q 速度由零增加到v过程
v=
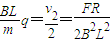
q=

答:(1)在绳未断前U形金属框架做匀加速运动t时刻水平拉力F的大小是ma+
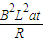 ,绳子断开后瞬间棒的加速度是
,绳子断开后瞬间棒的加速度是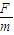 .
.(2)若在绳子断开的时刻立即撤去拉力F,框架和导体棒将怎样运动,它们的最终状态是框架向左匀速,棒向右匀速.
(3)在(2)的情景下,撤去拉力F后棒上产生的电热是
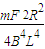 ,通过导体棒的电量是
,通过导体棒的电量是 .
.点评:本题考查了法拉第电磁感应定律、牛顿第二定律、能量守恒定律等多个知识点,要注意的是该题中框架NP和金属棒所在的磁场方向相反,从而所受安培力方向相同.

练习册系列答案
相关题目
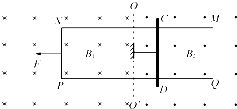 如图所示存在范围足够大的磁场区,虚线OO′为磁场边界,左侧为竖直向下的匀强磁场,磁感应强度为B1,右侧为竖直向上的磁感应强度为B2的匀强磁场区,B1=B2=B.有一质量为m且足够长的U形金属框架MNPQ平放在光滑的水平面上,框架跨过两磁场区,磁场边界OO′与框架的两平行导轨MN、PQ垂直,两导轨相距L,一质量也为m的金属棒垂直放置在右侧磁场区光滑的水平导轨上,并用一不可伸长的绳子拉住,绳子能承受的最大拉力是F0,超过F0绳子会自动断裂,已知棒的电阻是R,导轨电阻不计,t=0时刻对U形金属框架施加水平向左的拉力F让其从静止开始做加速度为a的匀加速直线运动.
如图所示存在范围足够大的磁场区,虚线OO′为磁场边界,左侧为竖直向下的匀强磁场,磁感应强度为B1,右侧为竖直向上的磁感应强度为B2的匀强磁场区,B1=B2=B.有一质量为m且足够长的U形金属框架MNPQ平放在光滑的水平面上,框架跨过两磁场区,磁场边界OO′与框架的两平行导轨MN、PQ垂直,两导轨相距L,一质量也为m的金属棒垂直放置在右侧磁场区光滑的水平导轨上,并用一不可伸长的绳子拉住,绳子能承受的最大拉力是F0,超过F0绳子会自动断裂,已知棒的电阻是R,导轨电阻不计,t=0时刻对U形金属框架施加水平向左的拉力F让其从静止开始做加速度为a的匀加速直线运动.