Question

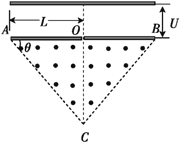
【题目】如图所示，在等腰三角形△ABC区域内有垂直纸面向外的匀强磁场，三角形的底边AB＝2L， θ＝45°，O为底边的中点。现有一质量为m、电荷量为q的带正电粒子从静止开始经过电势差为U的电场加速后，从O点垂直AB进入磁场，不计粒子的重力与空气阻力的影响。

(1)求粒子经电场加速后射入磁场时的速度。

(2)若已知磁感应强度大小，则粒子从何处射出磁场?

(3)磁感应强度B为多少时，粒子在磁场中能以最大的圆周半径偏转后打到OA板?

Answer 1

【答案】（1）（2）粒子从AC连线上距A点L处射出（3）B＝

【解析】

（1）由动能定理

qU＝mv2

解得：

v＝。

（2）粒子进入磁场后做匀速圆周运动，有：

qvB＝m

得

r＝＝L

故粒子从AC连线上距A点L处射出。

（3）要使粒子能射到OA连线上且半径最大，则粒子的轨迹应与AC边相切，如图所示。设此时粒子轨迹的半径为R，由几何关系有：

R+＝L

以及

qvB＝m

得

B＝。