题目内容
【题目】如图所示,光滑水平面上置有一个质量为 2m,高度为 h=1.25 m 的木板 A,木板左侧相距S=2 m 处固定一厚度不计高度与木板相同的挡板,挡板与木板 A 在同一条直线上。木板右侧边缘正上方相距 R 的 O 点系一细线,细线另一端系质量为 m=1 kg 可以视为质点的物块B,细线长度为 R=1.6 m,物体 B 与木板 A 间的动摩擦因数为μ=0.2。现把细线水平向右拉直,将物体 B 以竖直向下的速度 v0 =![]() 抛出,物体 B 运动到 O 点正下方时细线恰好拉断,物体 B 滑上木板 A。已知木板 A 与挡板相撞时,物体 B 恰好从木板 A 上水平抛出,重力加速度取 g=10 m/s2。计算:
抛出,物体 B 运动到 O 点正下方时细线恰好拉断,物体 B 滑上木板 A。已知木板 A 与挡板相撞时,物体 B 恰好从木板 A 上水平抛出,重力加速度取 g=10 m/s2。计算:
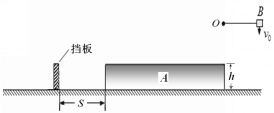
(1)细线能承受的最大拉力及计算木板 A 的长度;
(2)物体 B 从滑上木板 A 到落到水平面上所需的时间。
【答案】(1) 50N , 10m (2) 2.5s
【解析】
(1)物体B从释放到最低点,机械能守恒,由机械能守恒定律得:
![]()
由牛顿第二定律有:T-mg=m![]()
解得 ![]() T=5mg=50N
T=5mg=50N
设A与挡板碰撞前瞬间,A、B的速度分别为vA和vB,由动量守恒定律得:
mv1=mvB+2mvA
对A应用动能定理:![]()
联立解得:vB=4m/s vA=2m/s
设木板A的长度为L,对A、B系统根据能量守恒有:
![]()
解得L=10m
(2)物体 B 在木板 A 上的加速度a=![]() = 2m/s2
= 2m/s2
所以物体 B 在木板 A 上滑动的时间![]() = 2s
= 2s
物体 B 做平抛运动,竖直方向的分运动是自由落体运动,由 h =![]() gt22
gt22
解得 t2=0.5s
所以物体 B 从滑上木板 A 到落到水平面上所需的时间为 t = t1 + t2 = 2.5s

练习册系列答案
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案
相关题目