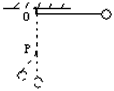题目内容
如图所示，将小球拉紧，悬线在水平位置无初速释放，当小球达到最低点时，细线被与悬点在同一竖直线上的小钉P挡住，则在悬线被钉子挡住的前后瞬间比较（ ）分析：由机械能守恒可知小球到达最低点的速度，小球碰到钉子后仍做圆周运动，由向心力公式可得出绳子的拉力与小球转动半径的关系；由圆周运动的性质可知其线速度、角速度及向心加速度的大小关系．
解答：解：A、在整个过程中只有重力做功，机械能守恒，悬线被小钉子挡住的前后，小球的机械能不变，故A错误；
B、悬线被小钉子挡住的前后，小球的线速度不变，则小球动能不变，故B错误；
C、小球做圆周运动，由牛顿第二定律得：F-mg=m
，悬线张力F=mg+m
，悬线被小钉子挡住的后，小球做圆周运动的半径r减小，则悬线张力变大，故C错误；
D、小球的向心加速度a=
，悬线被小钉子挡住的前后，小球速度v不变，轨道半径r减小，故向心加速度变大，故D正确；
故选D．
B、悬线被小钉子挡住的前后，小球的线速度不变，则小球动能不变，故B错误；
C、小球做圆周运动，由牛顿第二定律得：F-mg=m
| v2 |
| r |
| v2 |
| r |
D、小球的向心加速度a=
| v2 |
| r |
故选D．
点评：本题中要注意细绳碰到钉子前后转动半径的变化，再由向心力公式分析绳子上的拉力变化．
练习册系列答案
鹰派教辅衔接教材河北教育出版社系列答案
初中暑期衔接系列答案
相关题目
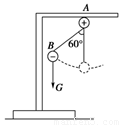
在一绝缘支架上，固定着一个带正电的小球A，A又通过一长为10cm的绝缘细绳连着另一个带负电的小球B，B的质量为0.1kg，电荷量为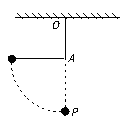
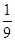×10－6C，如图所示，将小球B缓缓拉离竖直位置，当绳与竖直方向的夹角为60°时，将其由静止释放，小球B将在竖直面内做圆周运动．已知释放瞬间绳刚好张紧，但无张力．静电力常量
，g取10m/s2。求
