Question

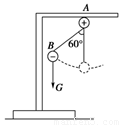
(13分)在一绝缘支架上，固定着一个带正电的小球A，A又通过一长为10cm的绝缘细绳连着另一个带负电的小球B，B的质量为0．1kg，电荷量为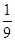×10^－6C，如图所示，将小球B缓缓拉离竖直位置，当绳与竖直方向的夹角为60°时，将其由静止释放，小球B将在竖直面内做圆周运动．已知释放瞬间绳刚好张紧，但无张力．静电力常量，g取10m/s²。求

（1）小球A的带电荷量；

（2）释放瞬间小球B的加速度大小；

（3）小球B运动到最低点时绳的拉力大小。

 

Answer 1

【答案】

见解析

【解析】

试题分析：（1）小球B刚释放瞬间，因v＝0  故垂直切线方向mgcos60°=

代入数值，得q_A＝5×10^－6C   （4分）

（2）切线方向， 则（4分）

（3）因释放后小球B做圆周运动，两球的相对距离不变，库仑力不做功，

由机械能守恒得mg（L－Lcos60°）＝

由最低点F_T＋－mg＝  由以上各式得：F_T＝mg＝1．5N（5分）

考点：牛顿第二定律，库仑定律，机械能守恒定律